РЕШУ ЦТ — математика–11

Задания

Задание № 1255 Добавить в вариант

Классификатор алгебры: 3.10. Правильная треугольная призма, 3.19. Шар, 4.2. Объем многогранника

Методы алгебры: Теорема Пифагора, Теорема синусов

Задания на 8 баллов

Правильная треугольная призма со стороной основания 3 см вписана в шар. Найдите объем призмы, если радиус шара $2 корень из 3$ см.

Решение. Рассмотрим сечение шара плоскостью основания призмы. Это круг, в который вписан равносторонний треугольник со стороной 3. По теореме синусов его радиус можно найти по формуле:

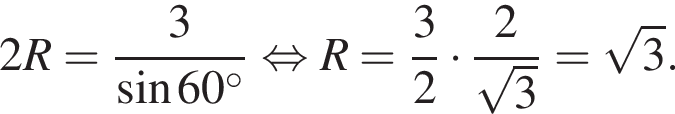
$2R= дробь: числитель: 3, знаменатель: синус 60 градусов конец дроби равносильно R= дробь: числитель: 3, знаменатель: 2 конец дроби умножить на дробь: числитель: 2, знаменатель: корень из: начало аргумента: 3 конец аргумента конец дроби = корень из: начало аргумента: 3 конец аргумента .$

Пусть O₁  — центр этого круга, O  — центр шара, A  — одна из вершин призмы. Тогда треугольник OO₁A  — прямоугольный и

$OO_1= корень из: начало аргумента: OA в квадрате минус O_1A в квадрате конец аргумента =$
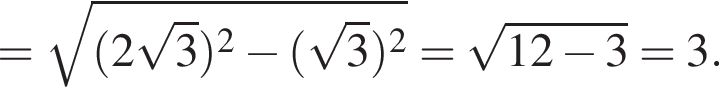
$= корень из: начало аргумента: левая круглая скобка 2 корень из: начало аргумента: 3 конец аргумента правая круглая скобка в квадрате минус левая круглая скобка корень из: начало аргумента: 3 конец аргумента правая круглая скобка в квадрате конец аргумента = корень из: начало аргумента: 12 минус 3 конец аргумента =3.$ $OO_1= корень из: начало аргумента: OA в квадрате минус O_1A в квадрате конец аргумента =$
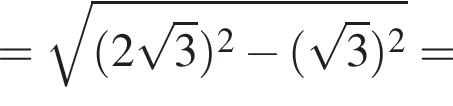
$= корень из: начало аргумента: левая круглая скобка 2 корень из: начало аргумента: 3 конец аргумента правая круглая скобка в квадрате минус левая круглая скобка корень из: начало аргумента: 3 конец аргумента правая круглая скобка в квадрате конец аргумента =$
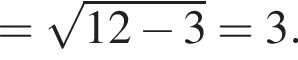
$= корень из: начало аргумента: 12 минус 3 конец аргумента =3.$

Итак, расстояние от центра шара до плоскости основания призмы равно 3, значит, высота призмы равна 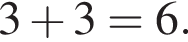$3 плюс 3=6.$ Тогда объем призмы равен:

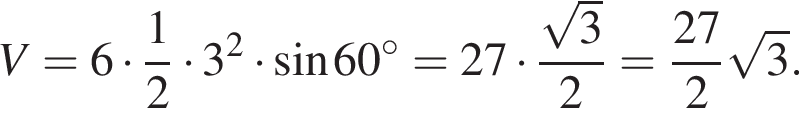
$V = 6 умножить на дробь: числитель: 1, знаменатель: 2 конец дроби умножить на 3 в квадрате умножить на синус 60 градусов =27 умножить на дробь: числитель: корень из: начало аргумента: 3 конец аргумента , знаменатель: 2 конец дроби = дробь: числитель: 27, знаменатель: 2 конец дроби корень из: начало аргумента: 3 конец аргумента .$

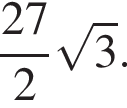
Ответ: $дробь: числитель: 27, знаменатель: 2 конец дроби корень из: начало аргумента: 3 конец аргумента .$

1255

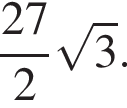
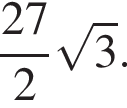
$дробь: числитель: 27, знаменатель: 2 конец дроби корень из: начало аргумента: 3 конец аргумента .$

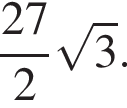
Классификатор алгебры: 3.10. Правильная треугольная призма, 3.19. Шар, 4.2. Объем многогранника

Методы алгебры: Теорема Пифагора, Теорема синусов

Ключ

№ п/п	№ задания	Ответ
1	1255	$дробь: числитель: 27, знаменатель: 2 конец дроби корень из: начало аргумента: 3 конец аргумента .$