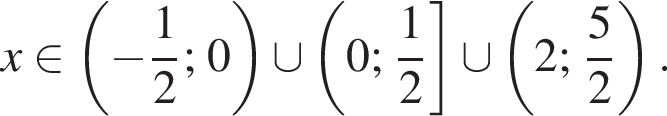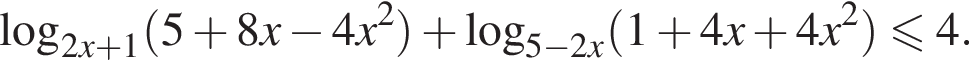
Ре­ше­ние. Пре­об­ра­зу­ем вы­ра­же­ние:

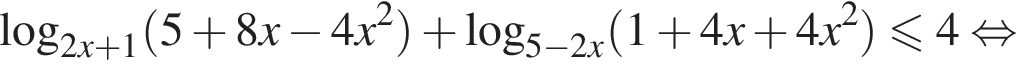
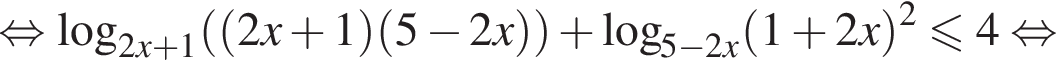
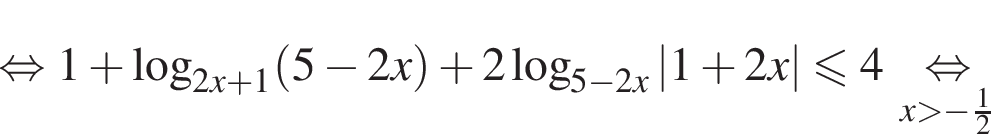
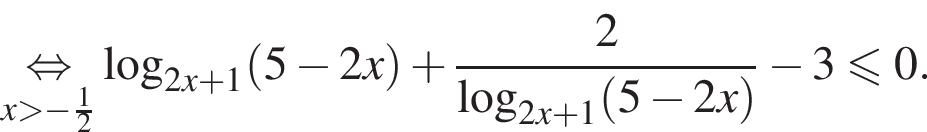
Пусть 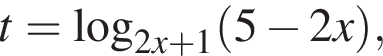тогда:

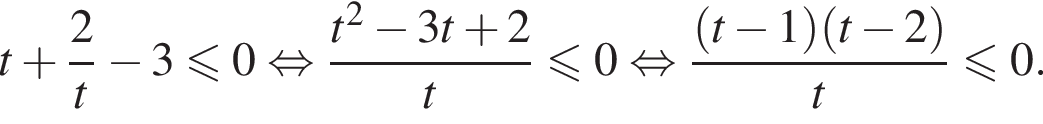
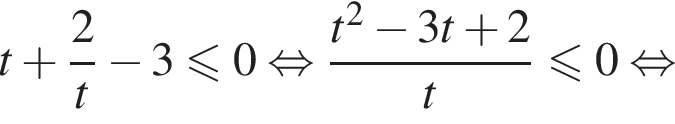
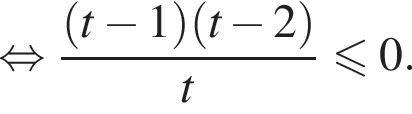
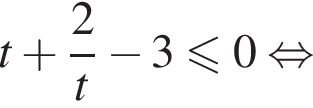
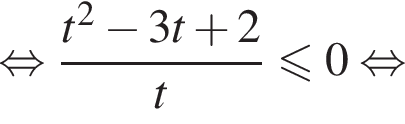
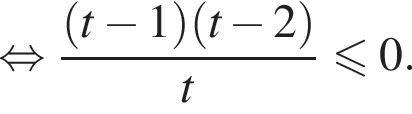
С по­мо­щью ме­то­да ин­тер­ва­лов по­лу­ча­ем, что:

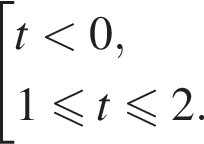
Вернёмся к ис­ход­ной пе­ре­мен­ной и решим пер­вое не­ра­вен­ство со­во­куп­но­сти:

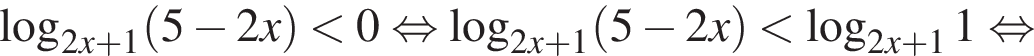
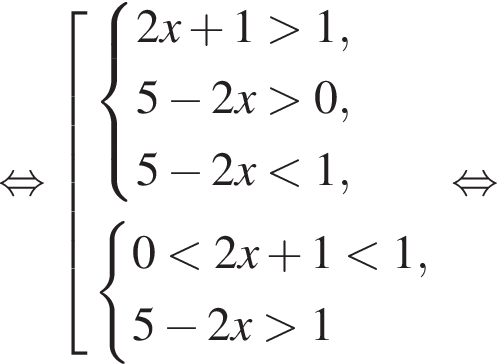
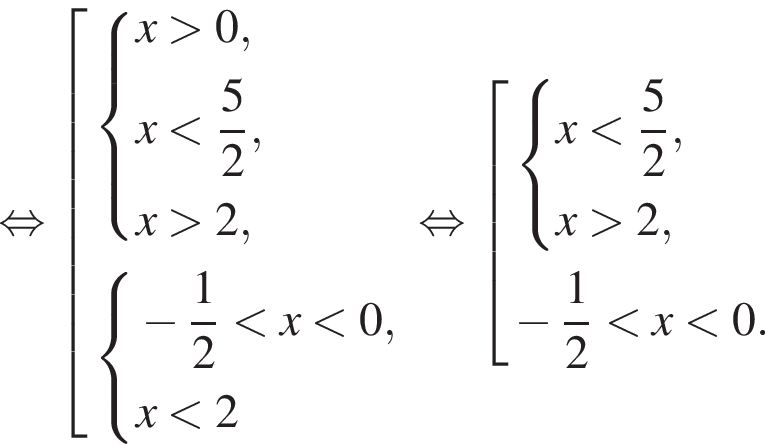
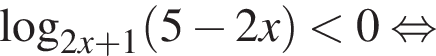
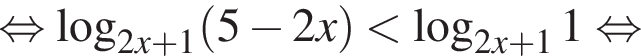
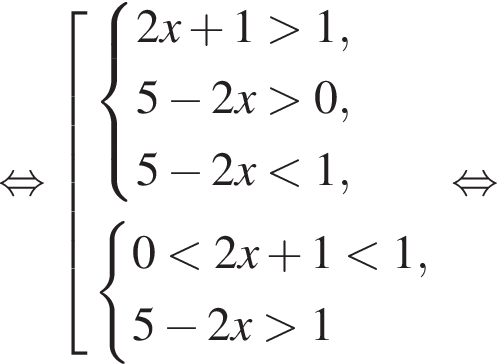
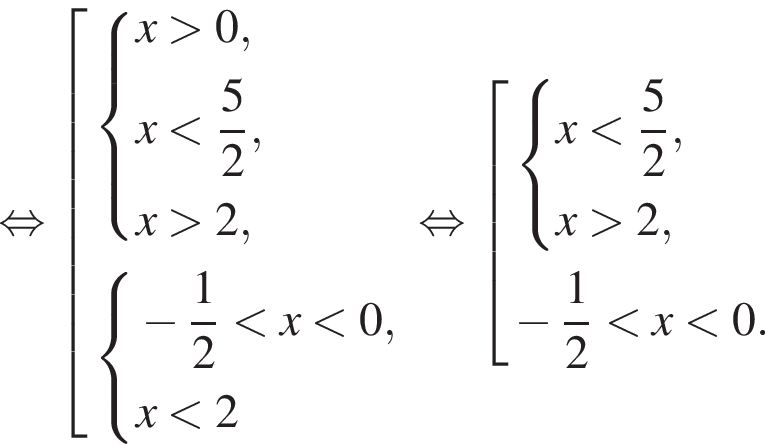
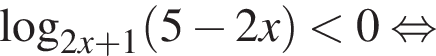
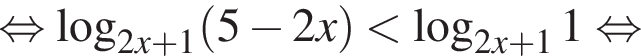
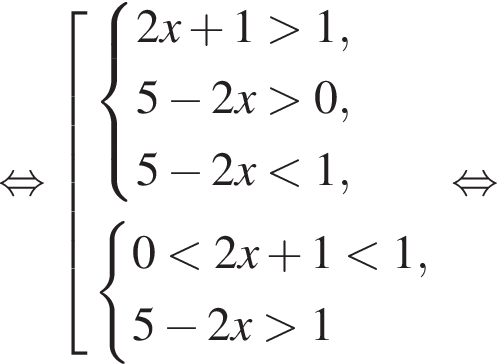
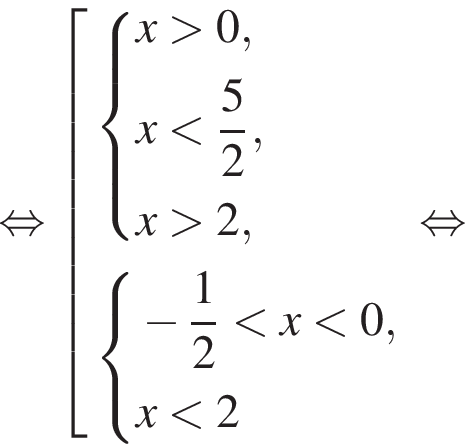
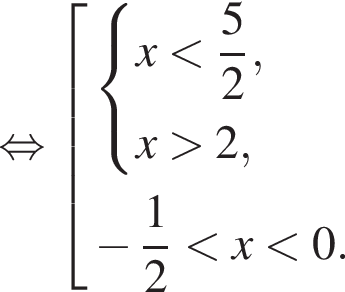
Те­перь решим вто­рое не­ра­вен­ство со­во­куп­но­сти:

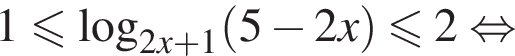
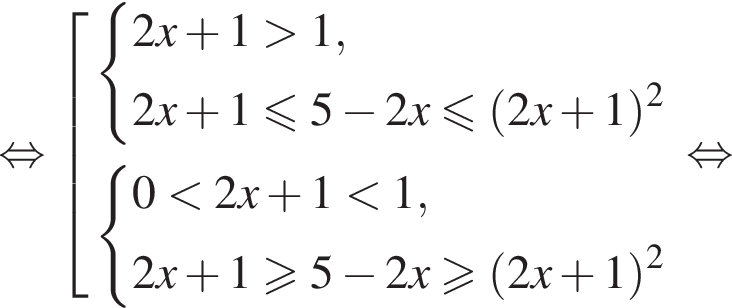
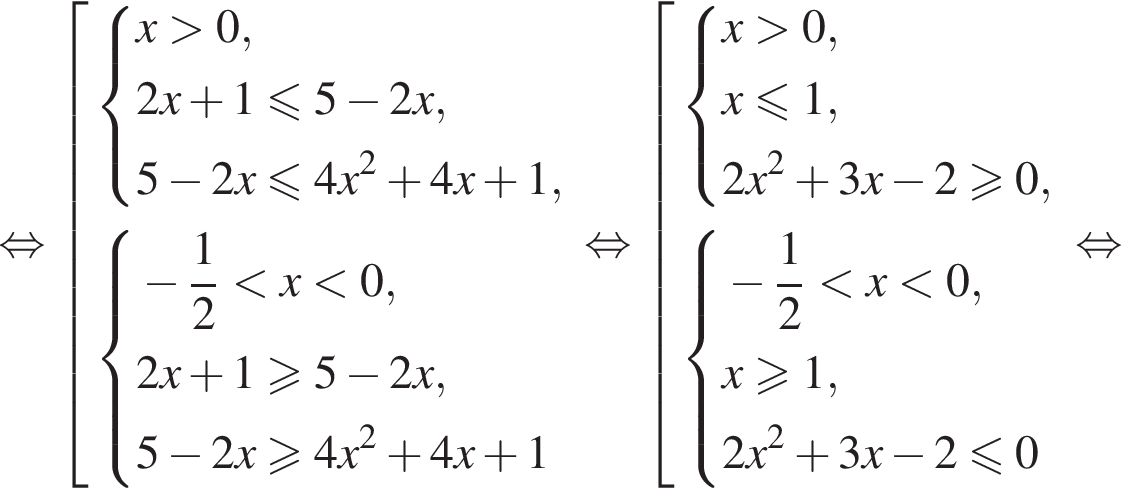
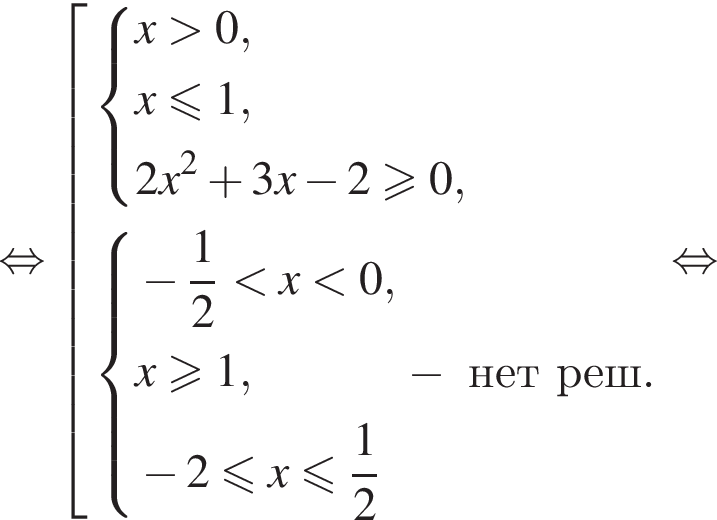
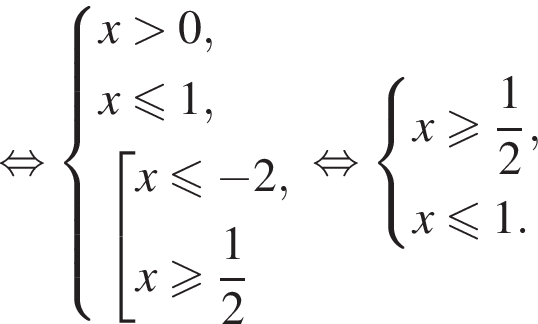
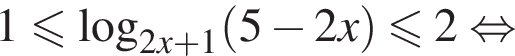
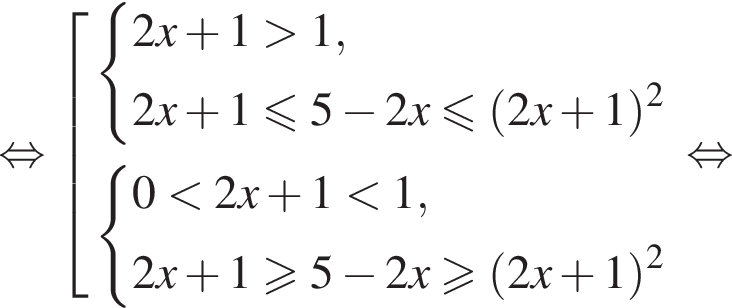
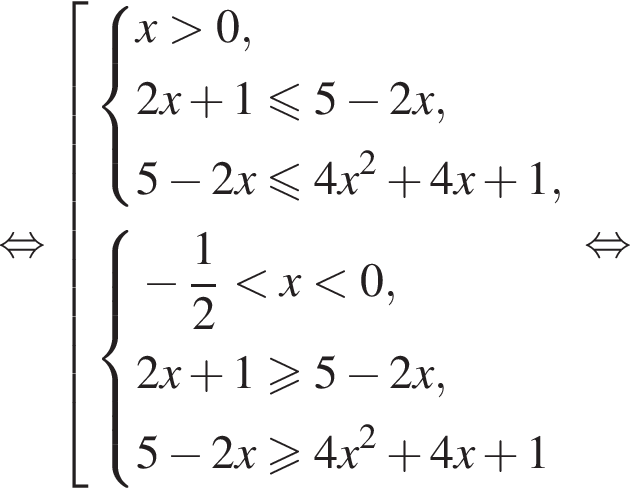
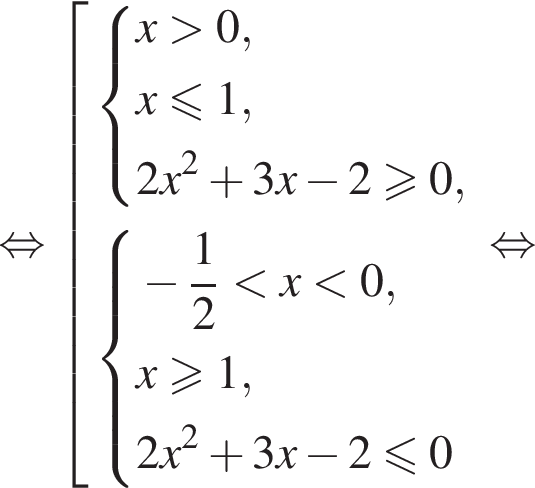
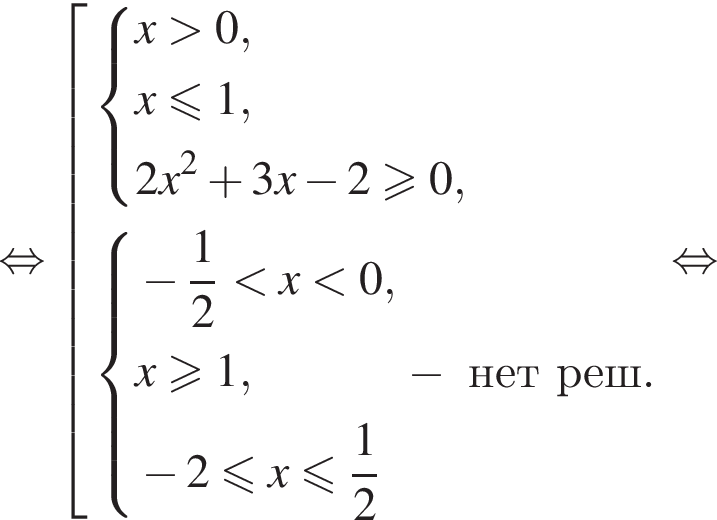
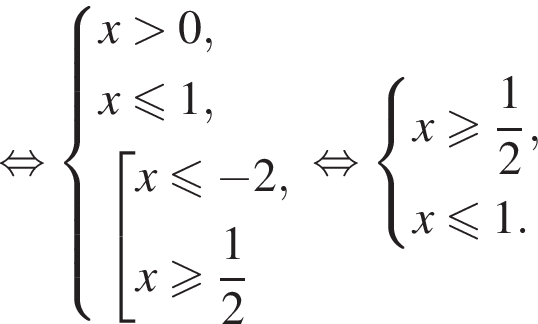
Ответ: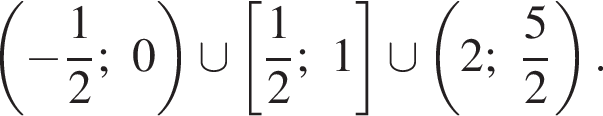

При­ве­дем дру­гое ре­ше­ние.

Пре­об­ра­зу­ем не­ра­вен­ство

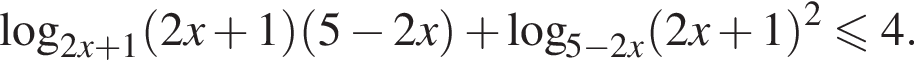
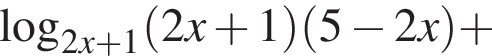
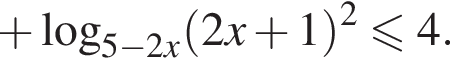
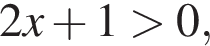
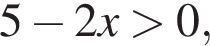
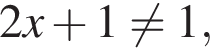
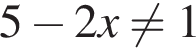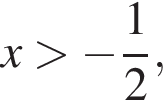
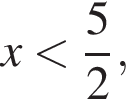
Для того, чтобы оно было опре­де­ле­но, не­об­хо­ди­мо и до­ста­точ­но вы­пол­не­ние усло­вий (по­ло­жи­тель­ность ар­гу­мен­тов ло­га­риф­мов будет сле­до­вать из пер­вых двух не­ра­венств). То есть Итак, ОДЗ не­ра­вен­ства это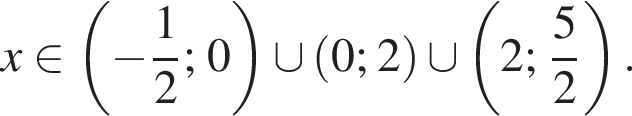

При этих усло­ви­ях пре­об­ра­зу­ем не­ра­вен­ство даль­ше

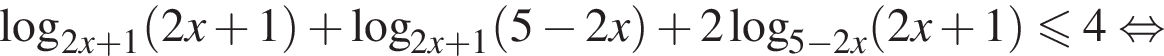
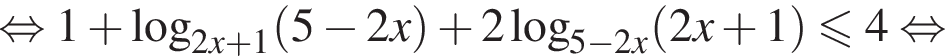
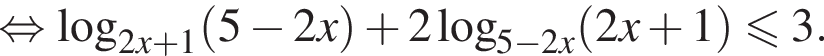
Обо­зна­чим вре­мен­но 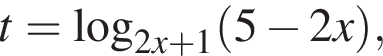тогда 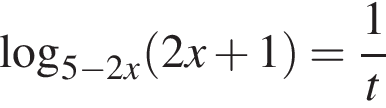и не­ра­вен­ство при­ни­ма­ет вид

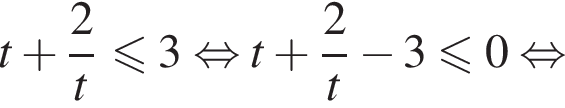
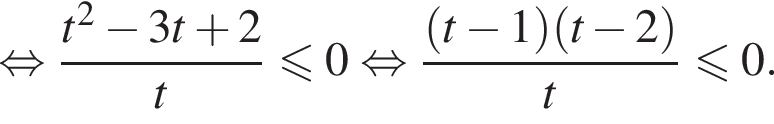
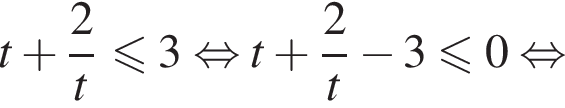
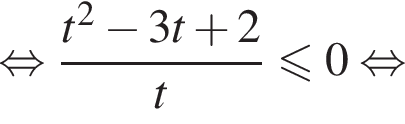
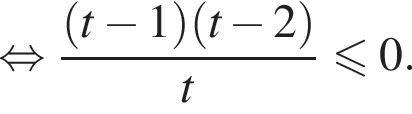
Зна­чит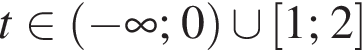

Раз­бе­рем пер­вый слу­чай, 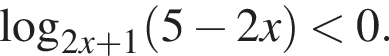При­ме­ним метод ра­ци­о­на­ли­за­ции:

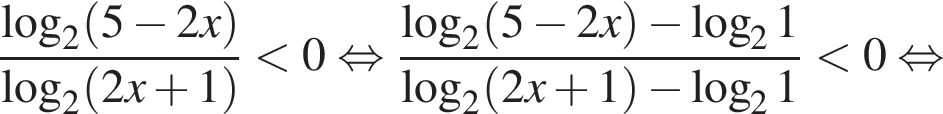
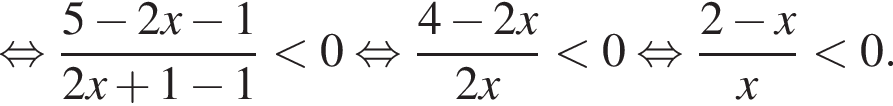
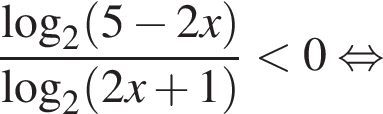
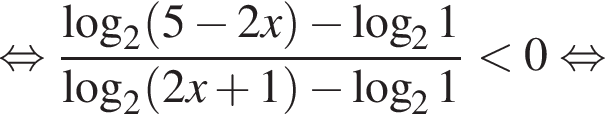
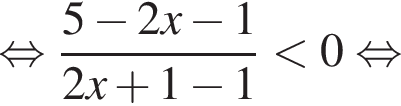
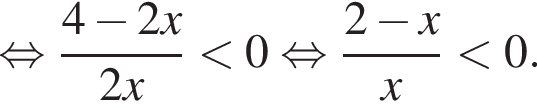
Это верно при и при Учи­ты­вая ОДЗ не­ра­вен­ства, по­лу­ча­ем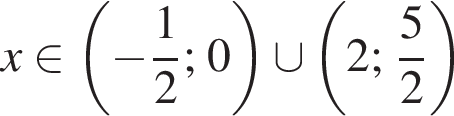

Те­перь раз­бе­рем вто­рой слу­чай, также при­ме­няя метод ра­ци­о­на­ли­за­ции

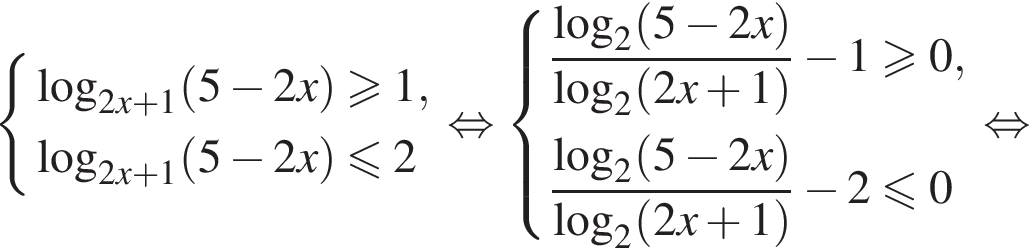
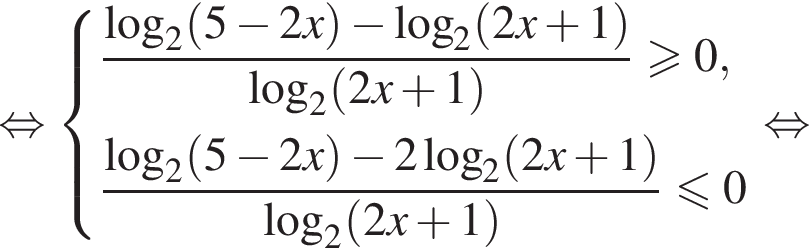
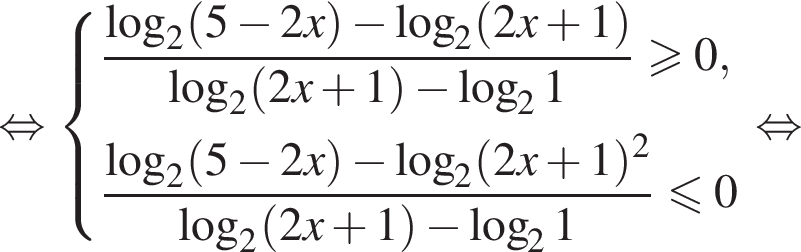
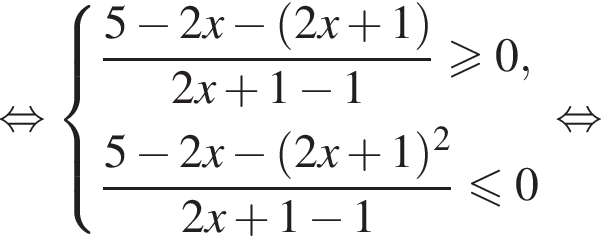
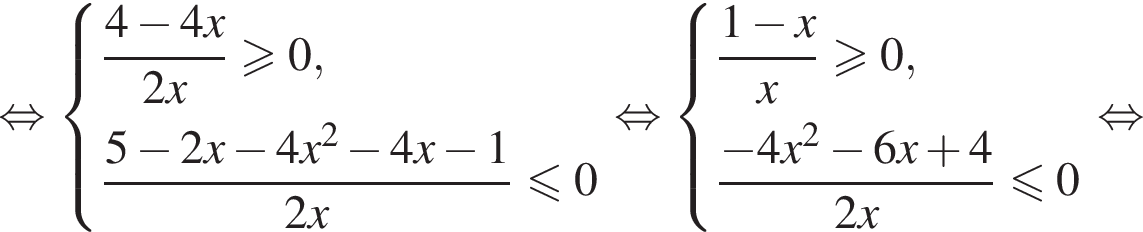
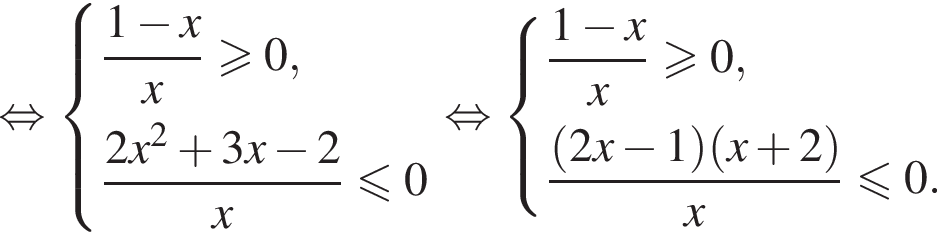
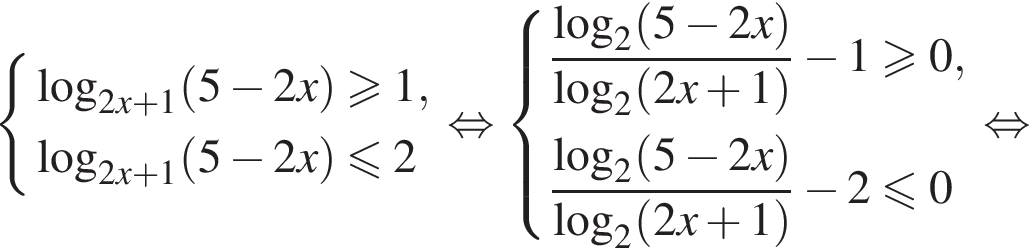
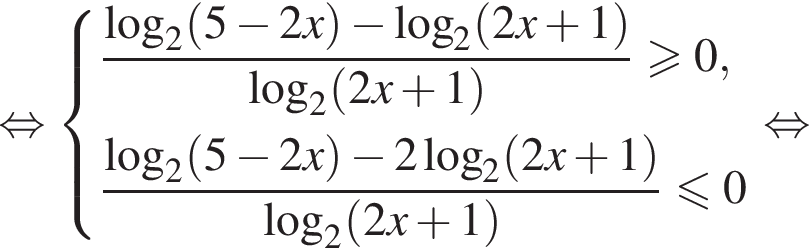
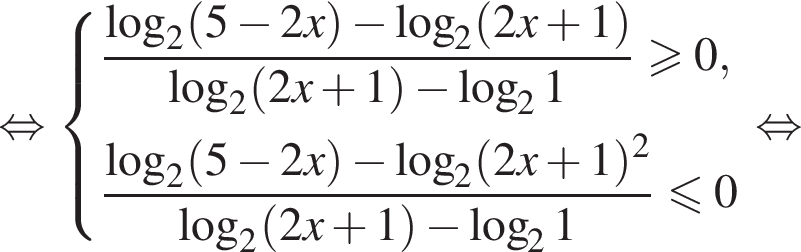
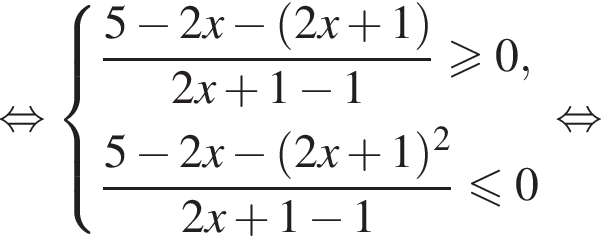
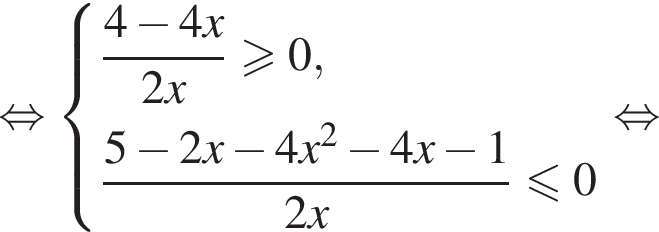
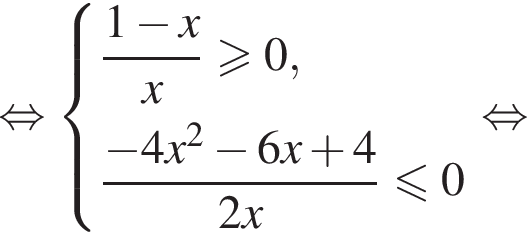
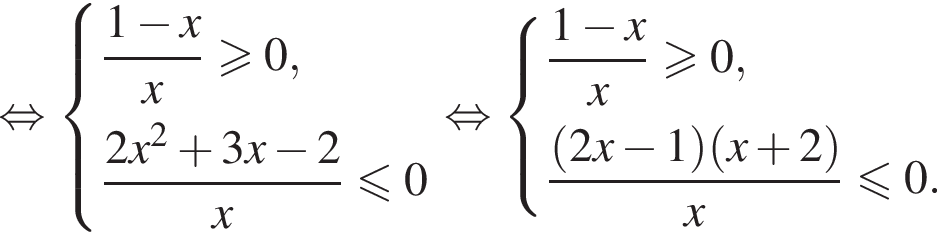
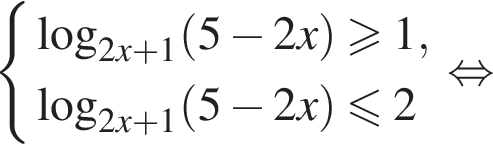
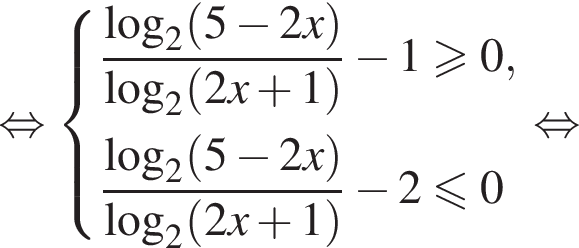
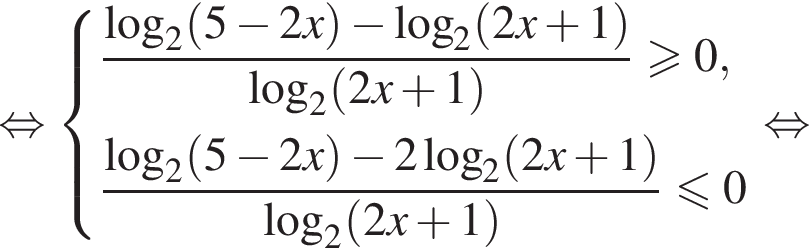
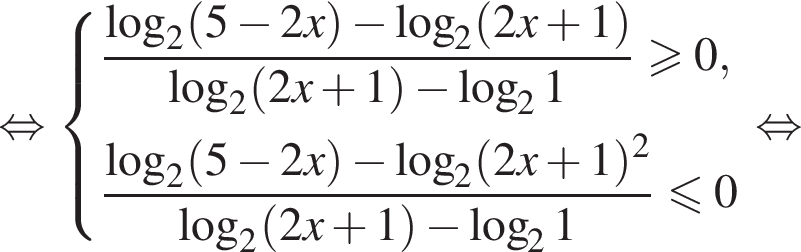
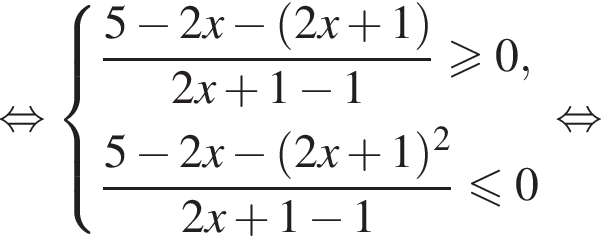
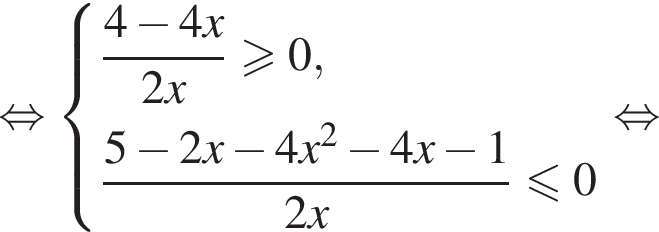
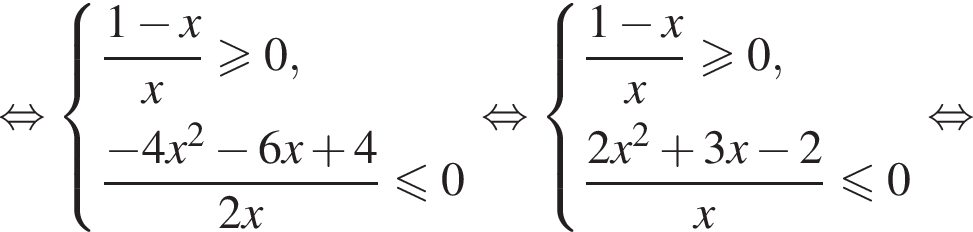
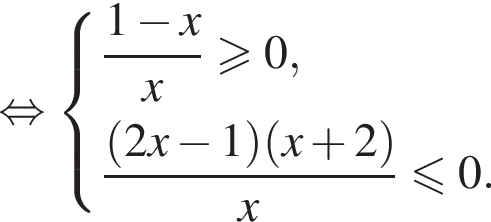
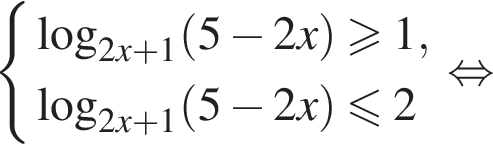
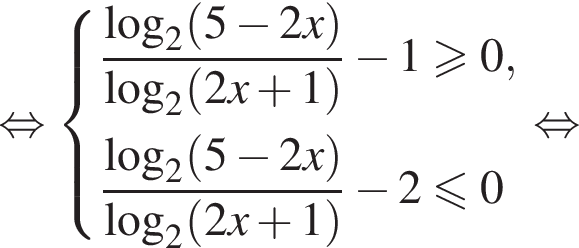
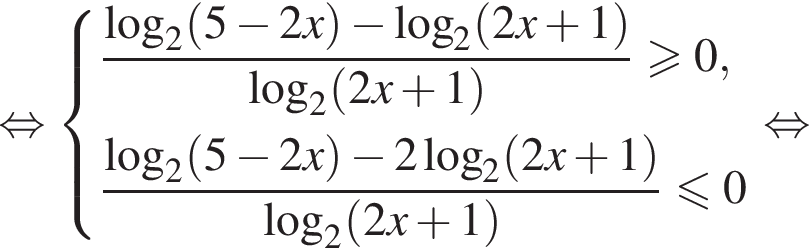
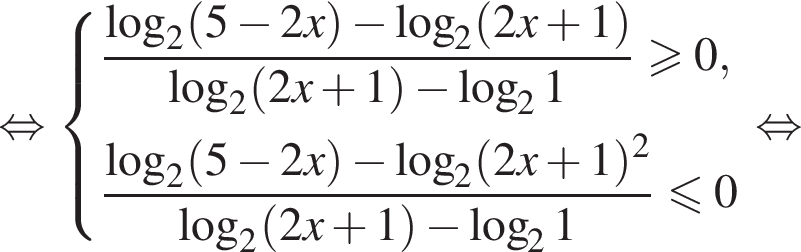
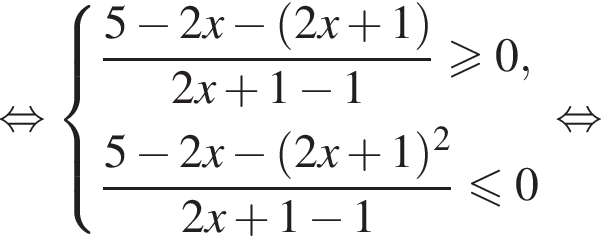
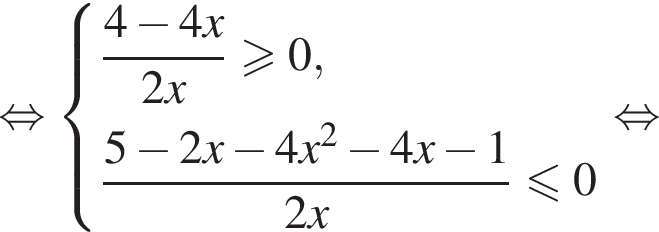
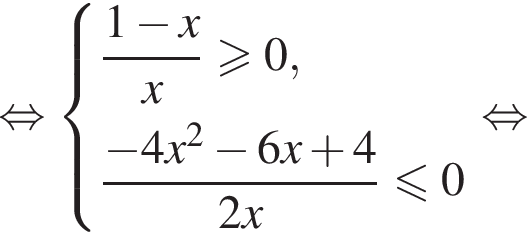
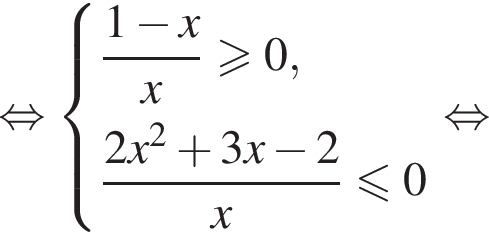
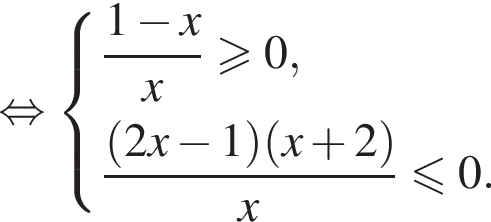
Пер­вое не­ра­вен­ство дает Вто­рое дает 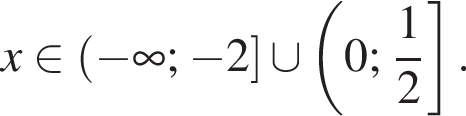Зна­чит, ре­ше­ни­ем си­сте­мы будет 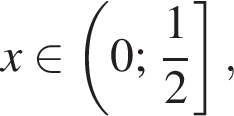при­чем весь этот про­ме­жу­ток вхо­дит в ОДЗ ис­ход­но­го не­ра­вен­ства.

Окон­ча­тель­но