РЕШУ ЦТ — математика–11

Задания

Задание № 1356 Добавить в вариант

Классификатор алгебры: 5.7. Уравнения с логарифмами по переменному основанию

Методы алгебры: Введение замены, Выделение полного квадрата, Группировка, разложение на множители

Задания на 9 баллов

Решите уравнение 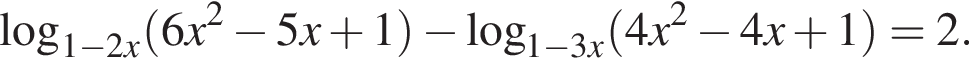$логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 6x в квадрате минус 5x плюс 1 правая круглая скобка минус логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 4x в квадрате минус 4x плюс 1 правая круглая скобка =2.$

Решение. Преобразуем уравнение:

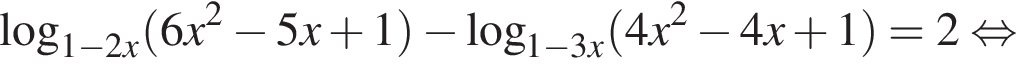
$логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 6x в квадрате минус 5x плюс 1 правая круглая скобка минус логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 4x в квадрате минус 4x плюс 1 правая круглая скобка =2 равносильно$
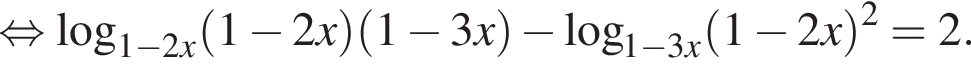
$равносильно логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка минус логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка в квадрате = 2.$

Для того, чтобы оно было определено, необходимо и достаточно выполнение условий:

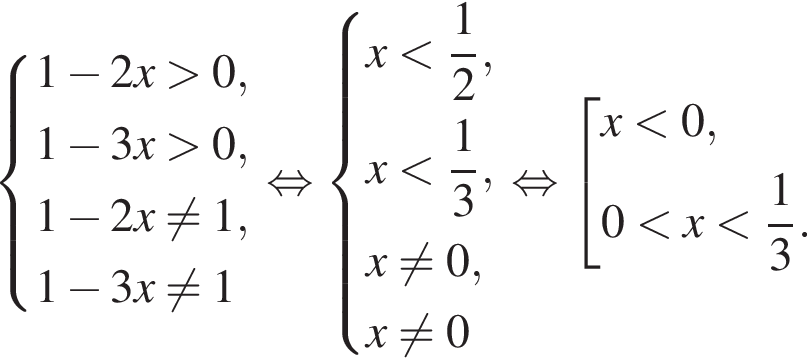
$система выражений 1 минус 2x больше 0,1 минус 3x больше 0,1 минус 2x не равно 1,1 минус 3x не равно 1 конец системы . равносильно система выражений x меньше дробь: числитель: 1, знаменатель: 2 конец дроби ,x меньше дробь: числитель: 1, знаменатель: 3 конец дроби ,x не равно 0,x не равно 0 конец системы . равносильно совокупность выражений x меньше 0,0 меньше x меньше дробь: числитель: 1, знаменатель: 3 конец дроби . 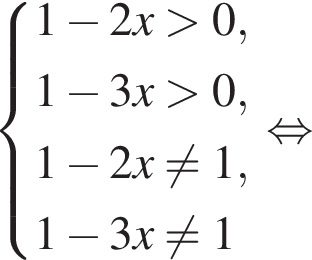конец совокупности .$ $система выражений 1 минус 2x больше 0,1 минус 3x больше 0,1 минус 2x не равно 1,1 минус 3x не равно 1 конец системы . равносильно$
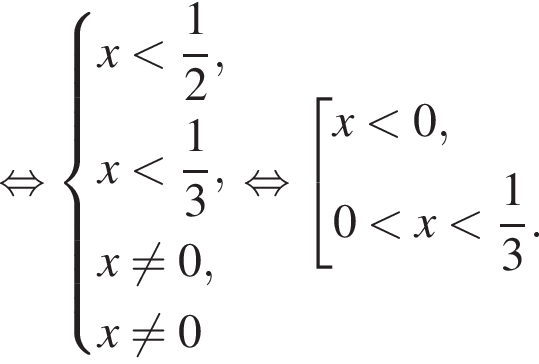
$равносильно система выражений x меньше дробь: числитель: 1, знаменатель: 2 конец дроби ,x меньше дробь: числитель: 1, знаменатель: 3 конец дроби ,x не равно 0,x не равно 0 конец системы . равносильно совокупность выражений x меньше 0,0 меньше x меньше дробь: числитель: 1, знаменатель: 3 конец дроби . конец совокупности .$

При этих условиях преобразуем уравнение дальше:

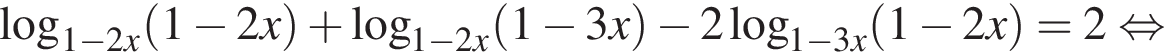
$логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка плюс логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка минус 2 логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка = 2 равносильно$
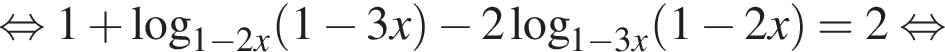
$равносильно 1 плюс логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка минус 2 логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка = 2 равносильно$
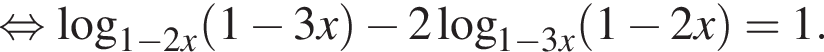
$равносильно логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка минус 2 логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка = 1.$

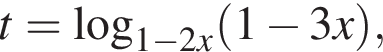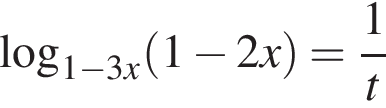Пусть $t= логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка ,$ тогда $логарифм по основанию левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка = дробь: числитель: 1, знаменатель: t конец дроби$ и уравнение принимает вид:

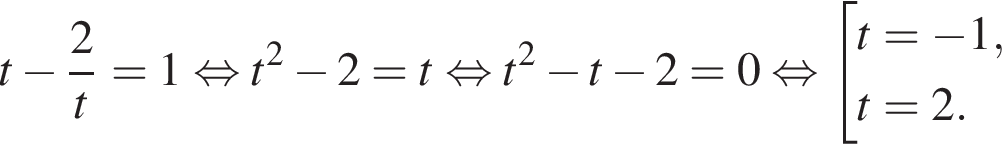
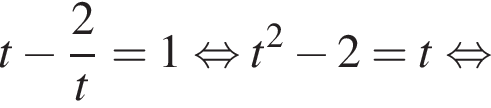
$t минус дробь: числитель: 2, знаменатель: t конец дроби =1 равносильно t в квадрате минус 2=t равносильно t в квадрате минус t минус 2=0 равносильно совокупность выражений t= минус 1,t=2. конец совокупности .$ $t минус дробь: числитель: 2, знаменатель: t конец дроби =1 равносильно t в квадрате минус 2=t равносильно$
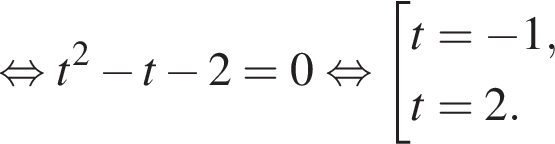
$равносильно t в квадрате минус t минус 2=0 равносильно совокупность выражений t= минус 1,t=2. конец совокупности .$

Вернёмся к исходной переменой и разберём каждый случай по отдельности.

Первый случай:

$логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка = минус 1 равносильно 1 минус 3x= дробь: числитель: 1, знаменатель: 1 минус 2x конец дроби равносильно$
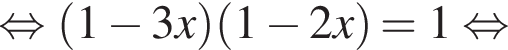
$равносильно левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка =1 равносильно$
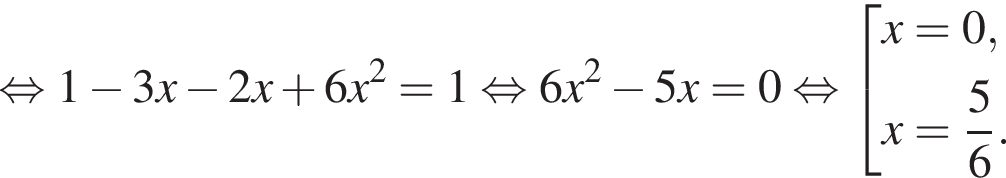
$равносильно 1 минус 3x минус 2x плюс 6x в квадрате =1 равносильно 6x в квадрате минус 5x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 5, знаменатель: 6 конец дроби . конец совокупности .$ $логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка = минус 1 равносильно 1 минус 3x= дробь: числитель: 1, знаменатель: 1 минус 2x конец дроби равносильно$
$равносильно левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка =1 равносильно 1 минус 3x минус 2x плюс 6x в квадрате =1 равносильно$
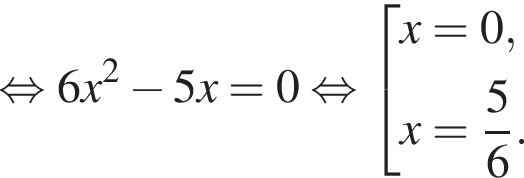
$равносильно 6x в квадрате минус 5x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 5, знаменатель: 6 конец дроби . конец совокупности .$ $логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка = минус 1 равносильно 1 минус 3x= дробь: числитель: 1, знаменатель: 1 минус 2x конец дроби равносильно$
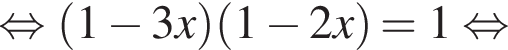
$равносильно левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка =1 равносильно$
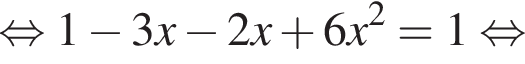
$равносильно 1 минус 3x минус 2x плюс 6x в квадрате =1 равносильно$
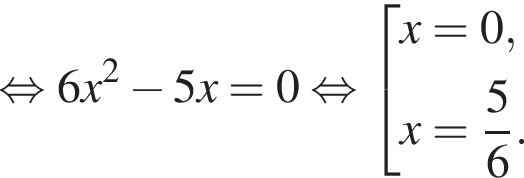
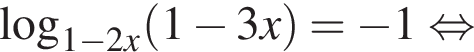
$равносильно 6x в квадрате минус 5x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 5, знаменатель: 6 конец дроби . конец совокупности .$ $логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка = минус 1 равносильно$
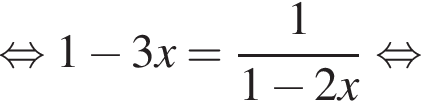
$равносильно 1 минус 3x= дробь: числитель: 1, знаменатель: 1 минус 2x конец дроби равносильно$
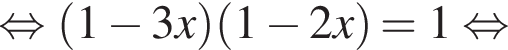
$равносильно левая круглая скобка 1 минус 3x правая круглая скобка левая круглая скобка 1 минус 2x правая круглая скобка =1 равносильно$
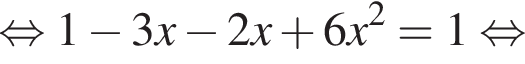
$равносильно 1 минус 3x минус 2x плюс 6x в квадрате =1 равносильно$
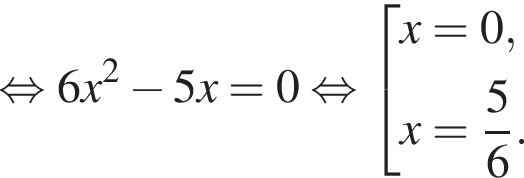
$равносильно 6x в квадрате минус 5x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 5, знаменатель: 6 конец дроби . конец совокупности .$

Но оба корня не входят в ОДЗ, поэтому они нам не подходят.

Второй случай:

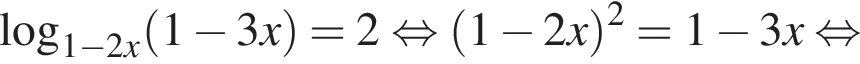
$логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка =2 равносильно левая круглая скобка 1 минус 2x правая круглая скобка в квадрате =1 минус 3x равносильно$
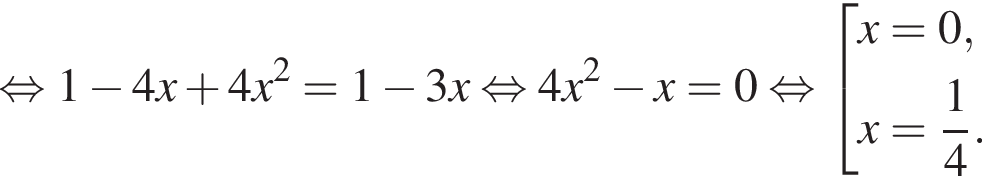
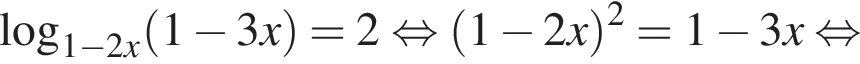
$равносильно 1 минус 4x плюс 4x в квадрате =1 минус 3x равносильно 4x в квадрате минус x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 1, знаменатель: 4 конец дроби . конец совокупности .$ $логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка =2 равносильно левая круглая скобка 1 минус 2x правая круглая скобка в квадрате =1 минус 3x равносильно$
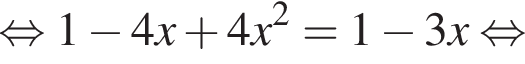
$равносильно 1 минус 4x плюс 4x в квадрате =1 минус 3x равносильно$
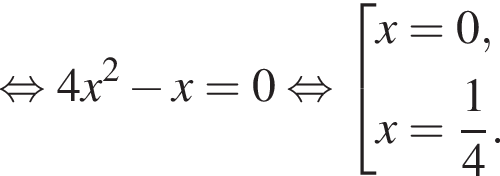
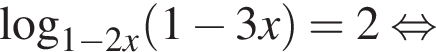
$равносильно 4x в квадрате минус x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 1, знаменатель: 4 конец дроби . конец совокупности .$ $логарифм по основанию левая круглая скобка 1 минус 2x правая круглая скобка левая круглая скобка 1 минус 3x правая круглая скобка =2 равносильно$
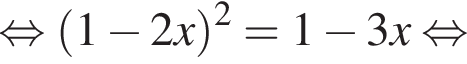
$равносильно левая круглая скобка 1 минус 2x правая круглая скобка в квадрате =1 минус 3x равносильно$
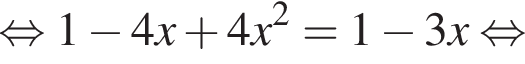
$равносильно 1 минус 4x плюс 4x в квадрате =1 минус 3x равносильно$
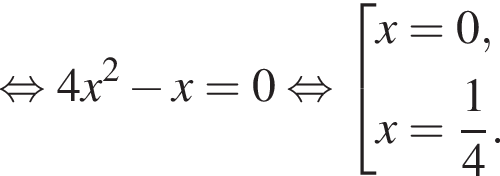
$равносильно 4x в квадрате минус x=0 равносильно совокупность выражений x=0,x= дробь: числитель: 1, знаменатель: 4 конец дроби . конец совокупности .$

Но корень x  =  0 не входит в ОДЗ и не подходит нам, а вот второй корень подходит.

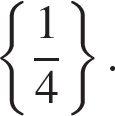
Ответ: $левая фигурная скобка дробь: числитель: 1, знаменатель: 4 конец дроби правая фигурная скобка .$

1356

$левая фигурная скобка дробь: числитель: 1, знаменатель: 4 конец дроби правая фигурная скобка .$

Классификатор алгебры: 5.7. Уравнения с логарифмами по переменному основанию

Методы алгебры: Введение замены, Выделение полного квадрата, Группировка, разложение на множители

Ключ

№ п/п	№ задания	Ответ
1	1356	$левая фигурная скобка дробь: числитель: 1, знаменатель: 4 конец дроби правая фигурная скобка .$