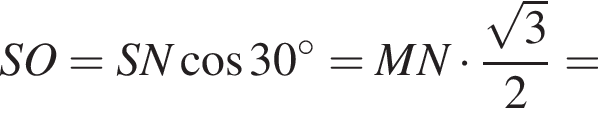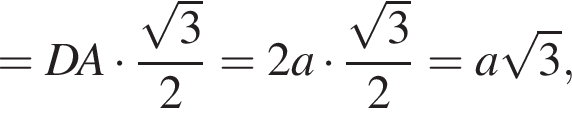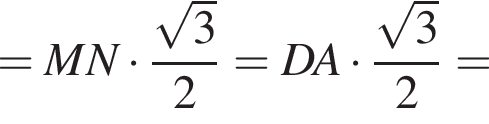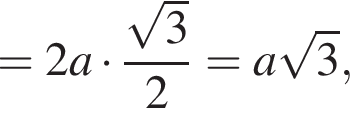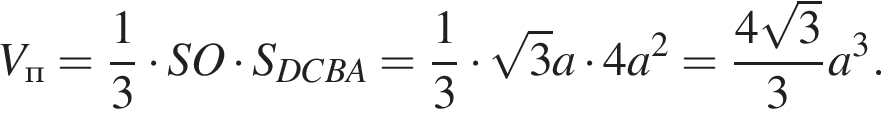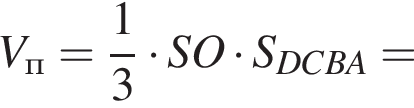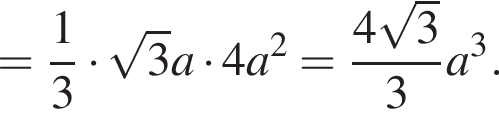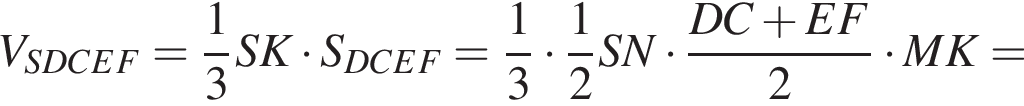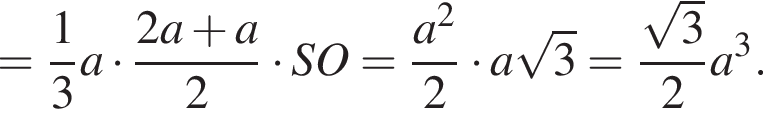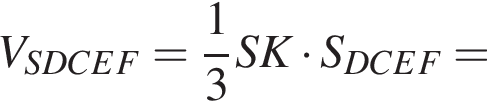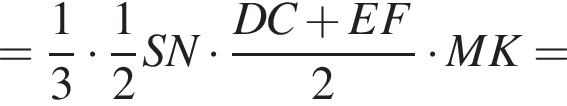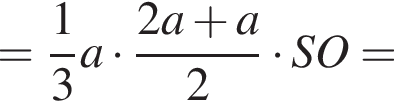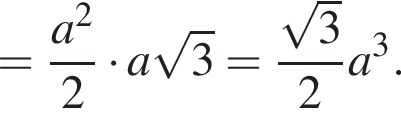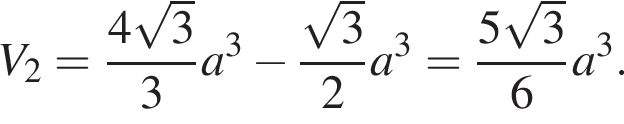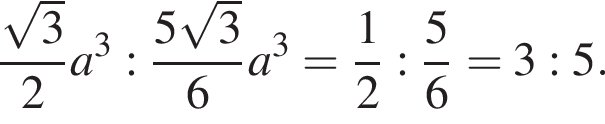Высота SO правильной четырехугольной пирамиды SABCD составляет с плоскостью боковой грани SAB угол 30°. Через сторону основания CD пирамиды проведена плоскость, перпендикулярная плоскости SAB. Найдите отношение объемов многогранников, полученных при пересечении пирамиды этой плоскостью.
Решение. Пусть O — центр основания пирамиды, M и N — середины ребер DC и BA соответственно, тогда плоскость SMN перпендикулярна BA, поскольку SO перпендикулярна BA и SN перпендикулярна BA. Опустим из O перпендикуляр на SN. Он будет лежать в плоскости MSN и потому будет перпендикулярен BA. Поскольку он еще и перпендикулярен SN, он будет перпендикулярен всей плоскости SBA. Значит, SN — проекция SO на грань SBA и потому  Значит,
Значит, 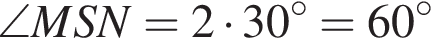 и треугольник SMN равносторонний, так как является равнобедренным с углом 60°.
и треугольник SMN равносторонний, так как является равнобедренным с углом 60°.
Пусть K, E и F — середины отрезков SN, SB и SA соответственно. Тогда MK — медиана и высота треугольника SMN. Кроме того, MK лежит в плоскости SMN, поэтому MK перпендикулярна BA. Значит, MK перпендикулярна плоскости SBA.
Значит, плоскость DCK, содержащая ее, перпендикулярна плоскости SBA. Поскольку EF параллельна BA и DC и точка K принадлежит EF, точки E и F лежат в этой же плоскости и сечением пирамиды будет трапеция DCEF.
Обозначим ребро основания пирамиды за 2a, тогда высота пирамиды равна:
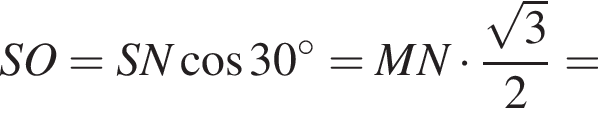
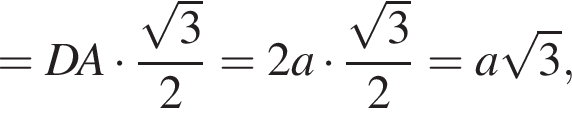

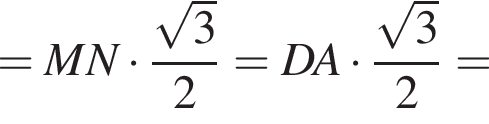
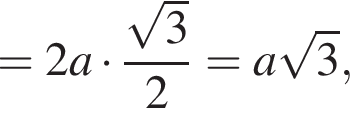
и объем пирамиды равен:
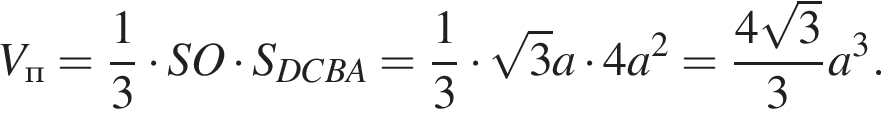
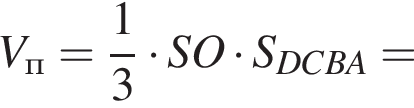
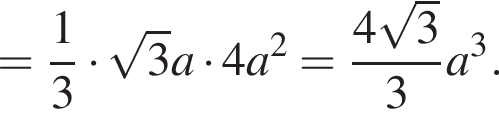
Найдем теперь объем пирамиды SDCEF. Заметим, что SK перпендикулярна MK и SK перпендикулярна FE, поэтому SK — высота пирамиды. Значит,
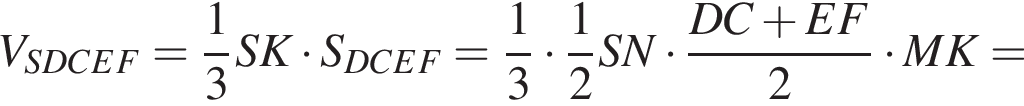
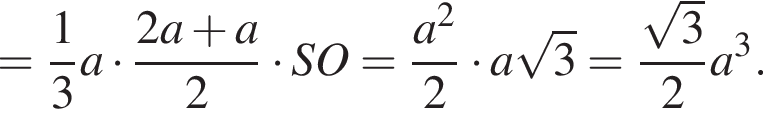
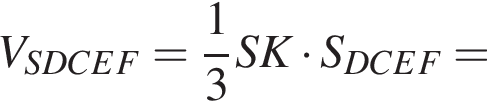
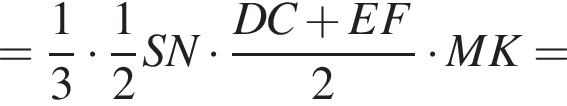
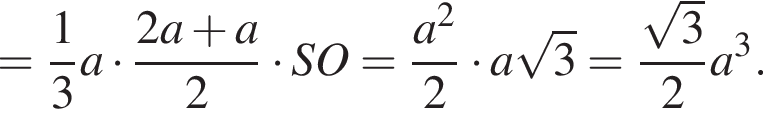
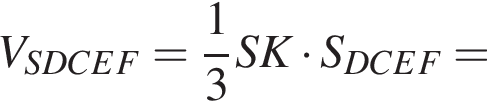
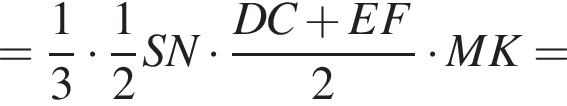
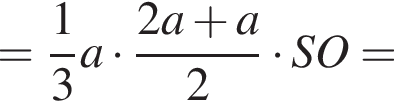
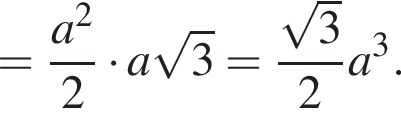
Тогда объем второй части пирамиды равен:
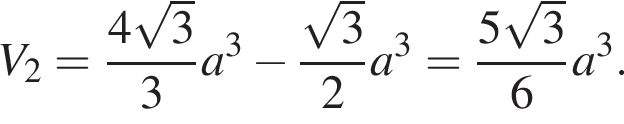
Наконец, искомое отношение равно:
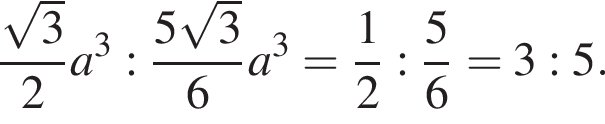
Ответ: 3 : 5.
Ответ: 3 : 5.

 Значит,
Значит, 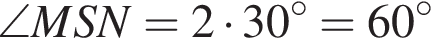 и треугольник SMN равносторонний, так как является равнобедренным с углом 60°.
и треугольник SMN равносторонний, так как является равнобедренным с углом 60°.