РЕШУ ЦТ — математика–11

Задания

Задание № 1396 Добавить в вариант

Классификатор алгебры: 4.7. Показательные уравнения других типов, 6.2. Тригонометрические уравнения, сводимые к целым на синус или косинус

Методы алгебры: Введение замены

Задания на 9 баллов

Найдите наибольший отрицательный корень уравнения

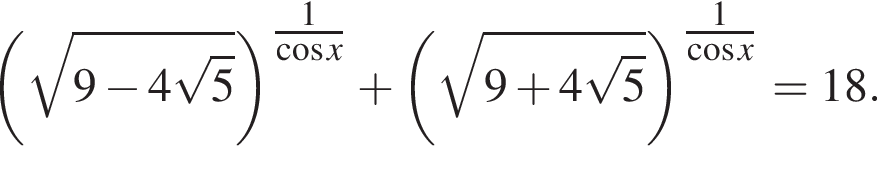
$левая круглая скобка корень из: начало аргумента: 9 минус 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac1 правая круглая скобка косинус x плюс левая круглая скобка корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac1 правая круглая скобка косинус x=18.$ $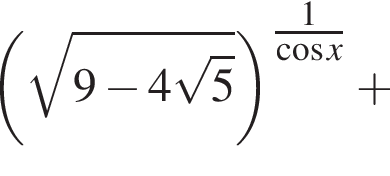левая круглая скобка корень из: начало аргумента: 9 минус 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac1 правая круглая скобка косинус x плюс$
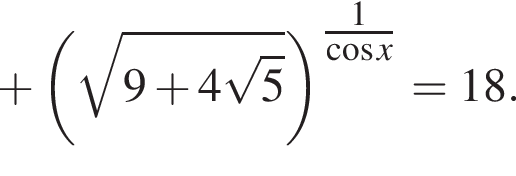
$плюс левая круглая скобка корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac1 правая круглая скобка косинус x=18.$

Решение. Заметим, что

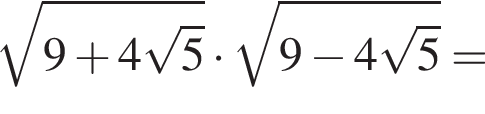
$корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента умножить на корень из: начало аргумента: 9 минус 4 корень из: начало аргумента: 5 конец аргумента конец аргумента =$
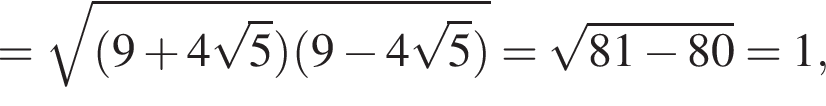
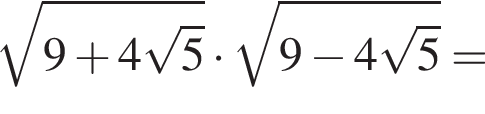
$= корень из: начало аргумента: левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка левая круглая скобка 9 минус 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка конец аргумента = корень из: начало аргумента: 81 минус 80 конец аргумента =1,$ $корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента умножить на корень из: начало аргумента: 9 минус 4 корень из: начало аргумента: 5 конец аргумента конец аргумента =$
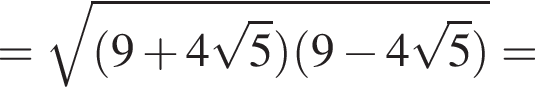
$= корень из: начало аргумента: левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка левая круглая скобка 9 минус 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка конец аргумента =$
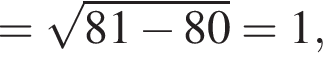
$= корень из: начало аргумента: 81 минус 80 конец аргумента =1,$

поэтому два слагаемых левой части взаимно обратны. Обозначим их временно t и $дробь: числитель: 1, знаменатель: t конец дроби ,$ получим:

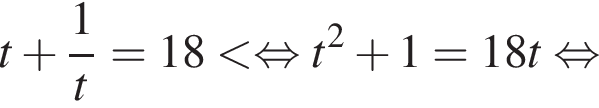
$t плюс дробь: числитель: 1, знаменатель: t конец дроби =18 меньше равносильно t в квадрате плюс 1=18t равносильно$
$равносильно t в квадрате минус 18t плюс 1=0 равносильно t= дробь: числитель: 18\pm корень из: начало аргумента: 18 в квадрате минус 4 конец аргумента , знаменатель: 2 конец дроби равносильно$
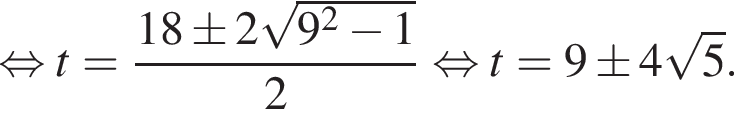
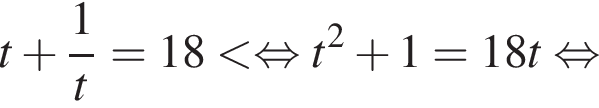
$равносильно t = дробь: числитель: 18\pm 2 корень из: начало аргумента: 9 в квадрате минус 1 конец аргумента , знаменатель: 2 конец дроби равносильно t = 9\pm 4 корень из: начало аргумента: 5 конец аргумента .$ $t плюс дробь: числитель: 1, знаменатель: t конец дроби =18 меньше равносильно t в квадрате плюс 1=18t равносильно$
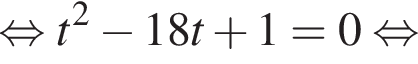
$равносильно t в квадрате минус 18t плюс 1=0 равносильно$
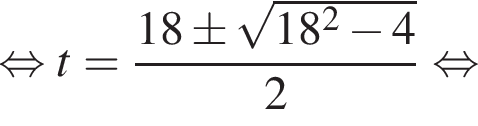
$равносильно t= дробь: числитель: 18\pm корень из: начало аргумента: 18 в квадрате минус 4 конец аргумента , знаменатель: 2 конец дроби равносильно$
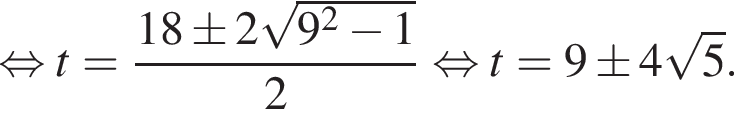
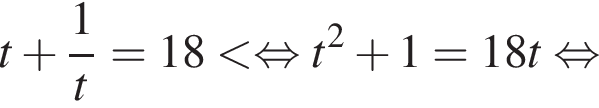
$равносильно t = дробь: числитель: 18\pm 2 корень из: начало аргумента: 9 в квадрате минус 1 конец аргумента , знаменатель: 2 конец дроби равносильно t = 9\pm 4 корень из: начало аргумента: 5 конец аргумента .$ $t плюс дробь: числитель: 1, знаменатель: t конец дроби =18 меньше равносильно t в квадрате плюс 1=18t равносильно$
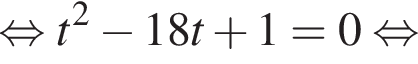
$равносильно t в квадрате минус 18t плюс 1=0 равносильно$
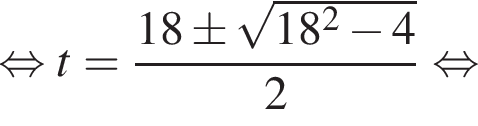
$равносильно t= дробь: числитель: 18\pm корень из: начало аргумента: 18 в квадрате минус 4 конец аргумента , знаменатель: 2 конец дроби равносильно$
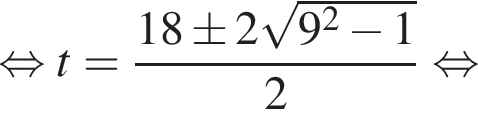
$равносильно t = дробь: числитель: 18\pm 2 корень из: начало аргумента: 9 в квадрате минус 1 конец аргумента , знаменатель: 2 конец дроби равносильно$
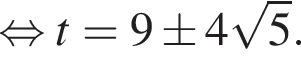
$равносильно t = 9\pm 4 корень из: начало аргумента: 5 конец аргумента .$

Значит, либо:

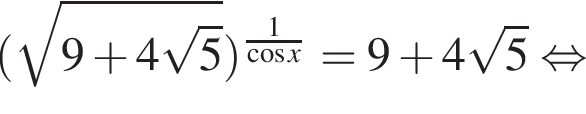
$левая круглая скобка корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка дробь: числитель: 1, знаменатель: косинус x конец дроби правая круглая скобка =9 плюс 4 корень из: начало аргумента: 5 конец аргумента равносильно$
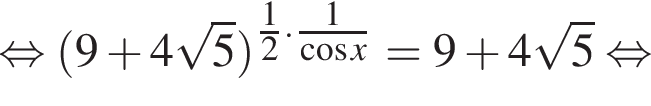
$равносильно левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac12 умножить на \tfrac1 правая круглая скобка косинус x=9 плюс 4 корень из: начало аргумента: 5 конец аргумента равносильно$
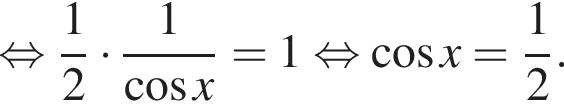
$равносильно дробь: числитель: 1, знаменатель: 2 конец дроби умножить на дробь: числитель: 1, знаменатель: косинус x конец дроби =1 равносильно косинус x= дробь: числитель: 1, знаменатель: 2 конец дроби .$

Полученное уравнение имеет наибольший отрицательный корень, равный $минус дробь: числитель: Пи , знаменатель: 3 конец дроби .$ Либо:

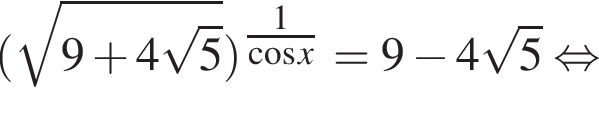
$левая круглая скобка корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac1 правая круглая скобка косинус x=9 минус 4 корень из: начало аргумента: 5 конец аргумента равносильно$
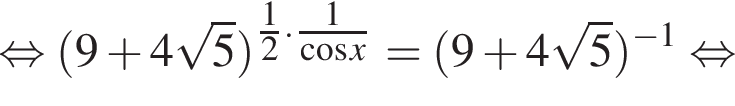
$равносильно левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac12 умножить на \tfrac1 правая круглая скобка косинус x= левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка в степени левая круглая скобка минус 1 правая круглая скобка равносильно$
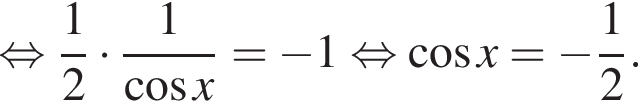
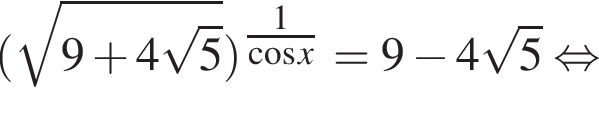
$равносильно дробь: числитель: 1, знаменатель: 2 конец дроби умножить на дробь: числитель: 1, знаменатель: косинус x конец дроби = минус 1 равносильно косинус x= минус дробь: числитель: 1, знаменатель: 2 конец дроби .$ $левая круглая скобка корень из: начало аргумента: 9 плюс 4 корень из: начало аргумента: 5 конец аргумента конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac1 правая круглая скобка косинус x=9 минус 4 корень из: начало аргумента: 5 конец аргумента равносильно$
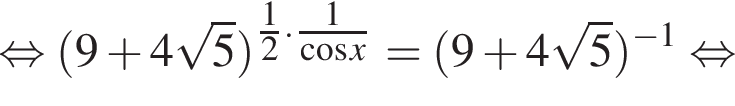
$равносильно левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка в степени левая круглая скобка \tfrac12 умножить на \tfrac1 правая круглая скобка косинус x= левая круглая скобка 9 плюс 4 корень из: начало аргумента: 5 конец аргумента правая круглая скобка в степени левая круглая скобка минус 1 правая круглая скобка равносильно$
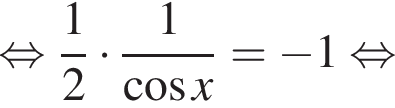
$равносильно дробь: числитель: 1, знаменатель: 2 конец дроби умножить на дробь: числитель: 1, знаменатель: косинус x конец дроби = минус 1 равносильно$
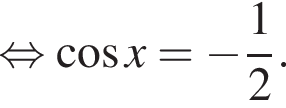
$равносильно косинус x= минус дробь: числитель: 1, знаменатель: 2 конец дроби .$

Полученное уравнение имеет наибольший отрицательны корень, равный $минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби .$

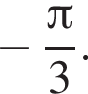
Ответ: $минус дробь: числитель: Пи , знаменатель: 3 конец дроби .$

1396

$минус дробь: числитель: Пи , знаменатель: 3 конец дроби .$

Методы алгебры: Введение замены

Ключ

№ п/п	№ задания	Ответ
1	1396	$минус дробь: числитель: Пи , знаменатель: 3 конец дроби .$