В пирамиду, основанием которой является равнобедренная трапеция, вписана сфера. Найдите площадь сферы, если основания трапеции равны 18 и 8, а высоты боковых граней, проведенные из вершины пирамиды, равны 12.
Решение. Пусть O — основание высоты пирамиды c вершиной S. Рассмотрим все треугольники с катетом SO и гипотенузой — одной из апофем граней. Все они равны по катету и гипотенузе, поэтому и второй катет у них одинаковый. По теореме о трех перпендикулярах этот второй катет, являющийся проекцией гипотенузы на плоскость основания, перпендикулярен соответствующему ребру основания, поэтому точка O равноудалена от всех сторон основания. Значит, она является центром вписанной в основание окружности. Поэтому суммы противоположных сторон трапеции равны, следовательно, ее боковая сторона равна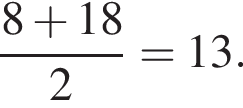 
Проведем в трапеции ABCD высоты BH и CK. Тогда
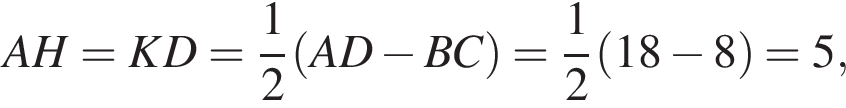
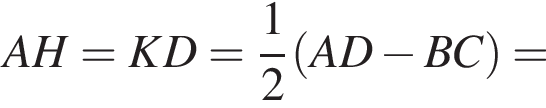
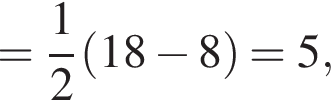
поэтому
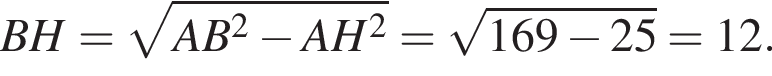
Высота трапеции равна диаметру ее вписанной окружности, поэтому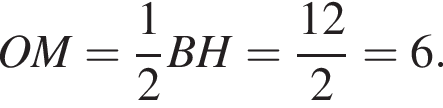 
Пусть M — середина BC, T — центр сферы, N — точка ее касания с плоскостью грани SBC, лежащая, на апофеме SM. Поскольку 
точка T лежит на биссектрисе угла SMO и, cледовательно, делит отрезок SO в отношении
Далее,
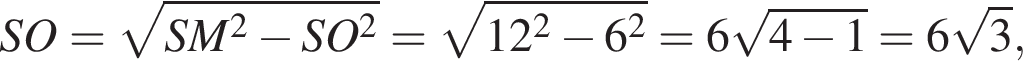
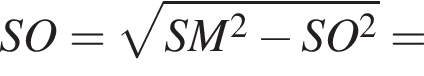
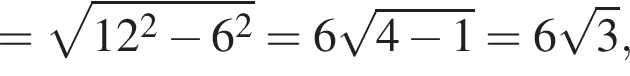
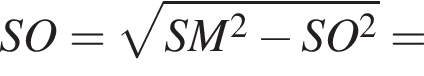
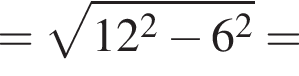
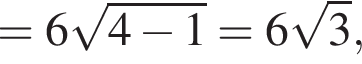
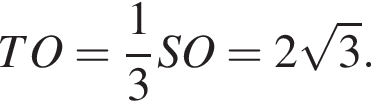
Наконец, площадь сферы равна:
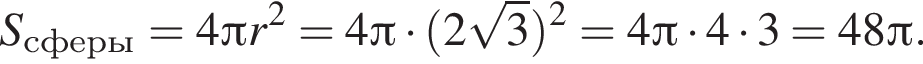
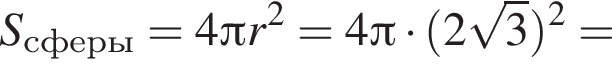
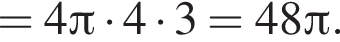
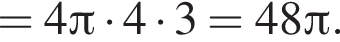
Ответ: 