Задание № 248 

Классификатор алгебры: 13.3. Монотонность и экстремумы функции , 13.4. Наибольшее и наименьшее значение функции, 15.8. Применение производной к исследованию функции
Задания на 8 баллов
i
Найдите промежутки возрастания и убывания, а также точки минимума и максимума функции 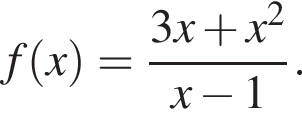
Решение. Вначале найдем область определения функции. Знаменатель оборачивается в ноль при ![]() значит,
значит,
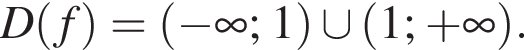
Теперь найдем ![]()
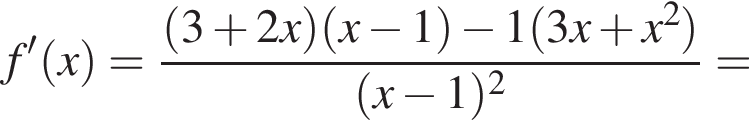
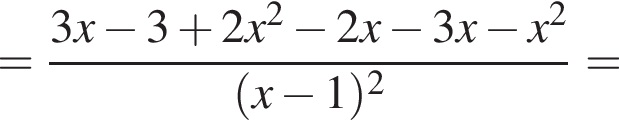
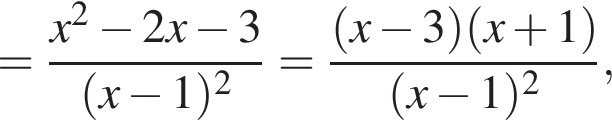

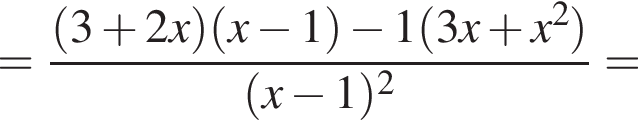
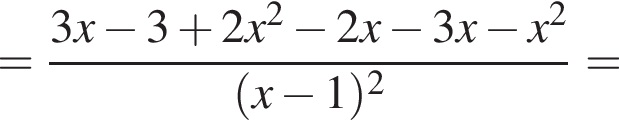
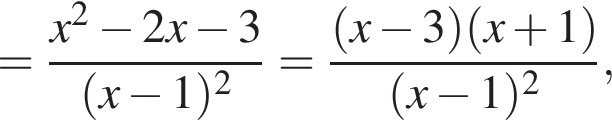

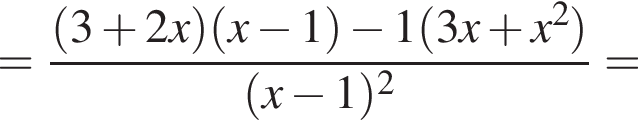
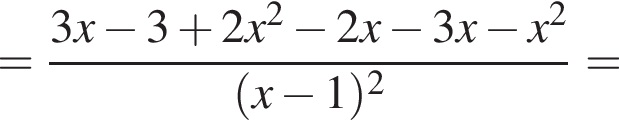
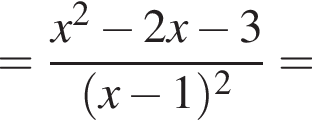
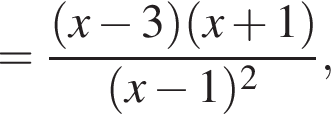
откуда  и
и 
Итак, функция возрастает на промежутке 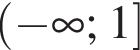 и на
и на  а убывает на промежутке
а убывает на промежутке 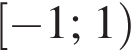 и на
и на ![]() (см. рис).
(см. рис).
Ответ: функция возрастает на промежутке 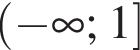 и на
и на  а убывает на промежутке
а убывает на промежутке 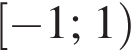 и на
и на ![]() Максимум и минимум функции соответственно равны
Максимум и минимум функции соответственно равны  и
и 
Ответ: функция возрастает на промежутке 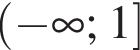 и на
и на  а убывает на промежутке
а убывает на промежутке 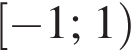 и на
и на 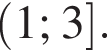 Максимум и минимум функции соответственно равны
Максимум и минимум функции соответственно равны  и
и 
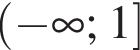 и на
и на  а убывает на промежутке
а убывает на промежутке 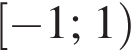 и на
и на  и
и 
248
функция возрастает на промежутке 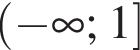 и на
и на  а убывает на промежутке
а убывает на промежутке 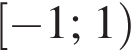 и на
и на 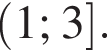 Максимум и минимум функции соответственно равны
Максимум и минимум функции соответственно равны  и
и 
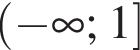 и на
и на  а убывает на промежутке
а убывает на промежутке 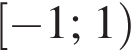 и на
и на  и
и 