РЕШУ ЦТ — математика–11

Задания

Задание № 318 Добавить в вариант

Классификатор алгебры: 6.3. Тригонометрические уравнения, сводимые к целым на тангенс или котангенс

Методы алгебры: Использование основного тригонометрического тождества и следствий из него, Сведение к однородному уравнению в тригонометрии, Формулы кратных углов

Задания на 8 баллов

Найдите количество корней уравнения 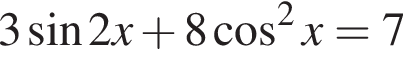$3 синус 2x плюс 8 косинус в квадрате x=7$ на промежутке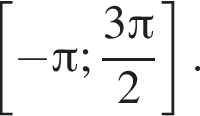 $левая квадратная скобка минус Пи ; дробь: числитель: 3 Пи , знаменатель: 2 конец дроби правая квадратная скобка .$

Решение. Домножим на тригонометрическую единицу:

$3 синус 2x плюс 8 косинус в квадрате x=7 равносильно$
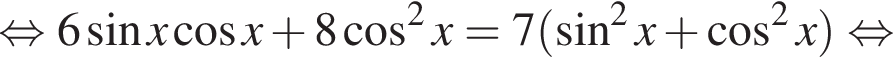
$равносильно 6 синус x косинус x плюс 8 косинус в квадрате x=7 левая круглая скобка синус в квадрате x плюс косинус в квадрате x правая круглая скобка равносильно$

$равносильно 6 синус x косинус x плюс 8 косинус в квадрате x минус 7 синус в квадрате x минус 7 косинус в квадрате x=0 равносильно$
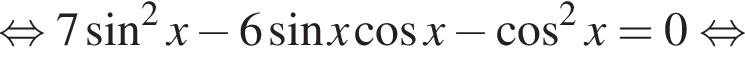
$равносильно 7 синус в квадрате x минус 6 синус x косинус x минус косинус в квадрате x=0 равносильно$

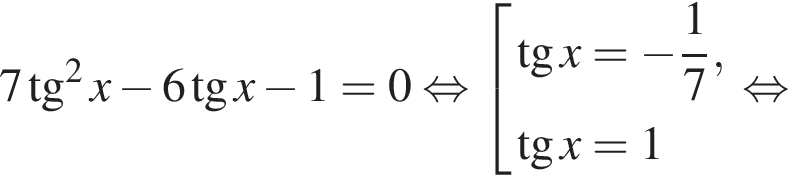
$7 тангенс в квадрате x минус 6 тангенс x минус 1=0 равносильно совокупность выражений тангенс x= минус дробь: числитель: 1, знаменатель: 7 конец дроби , тангенс x=1 конец совокупности . равносильно$
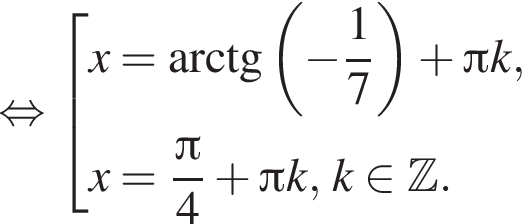
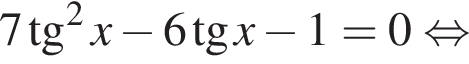
$равносильно совокупность выражений x= арктангенс левая круглая скобка минус дробь: числитель: 1, знаменатель: 7 конец дроби правая круглая скобка плюс Пи k, x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k, k принадлежит Z . конец совокупности .$ $7 тангенс в квадрате x минус 6 тангенс x минус 1=0 равносильно$
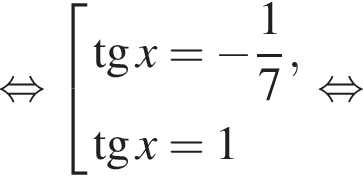
$равносильно совокупность выражений тангенс x= минус дробь: числитель: 1, знаменатель: 7 конец дроби , тангенс x=1 конец совокупности . равносильно$
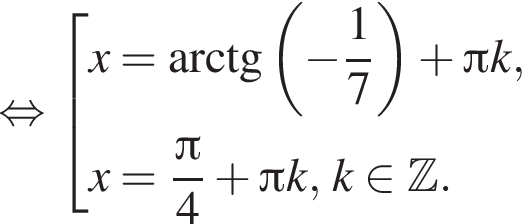
$равносильно совокупность выражений x= арктангенс левая круглая скобка минус дробь: числитель: 1, знаменатель: 7 конец дроби правая круглая скобка плюс Пи k, x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k, k принадлежит Z . конец совокупности .$

Заметим, что при домножении на $косинус x$ корни не потеряны.

Из графика видно, что на промежутке 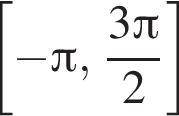$левая квадратная скобка минус Пи , дробь: числитель: 3 Пи , знаменатель: 2 конец дроби правая квадратная скобка$ исходное уравнение имеет 5 корней.

Ответ: 5.

318

Классификатор алгебры: 6.3. Тригонометрические уравнения, сводимые к целым на тангенс или котангенс

Ключ

№ п/п	№ задания	Ответ
1	318	5.