Ре­ше­ние. В ос­но­ва­нии пра­виль­ной тре­уголь­ной пи­ра­ми­ды лежит пра­виль­ный тре­уголь­ник, при­мем его сто­ро­ну за a. По усло­вию дву­гран­ный угол при бо­ко­вом ребре пра­виль­ной тре­уголь­ной пи­ра­ми­ды равен 120°, зна­чит, Тре­уголь­ник AKB  — рав­но­бед­рен­ный (AK  =  BK), тогда Вос­поль­зу­ем­ся тео­ре­мой си­ну­сов:

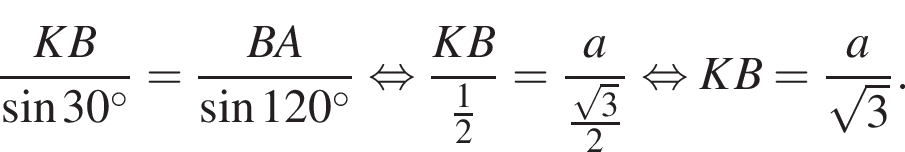
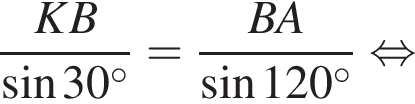
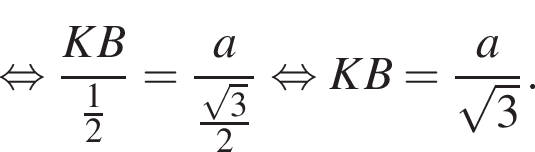
Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник BKC. Вос­поль­зу­ем­ся тео­ре­мой си­ну­сов:

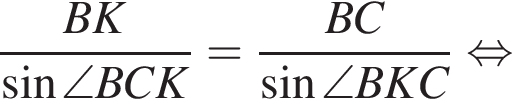
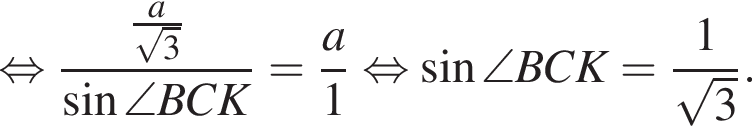
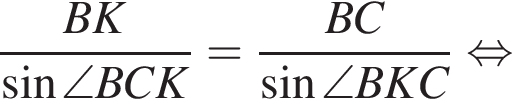
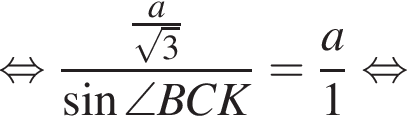
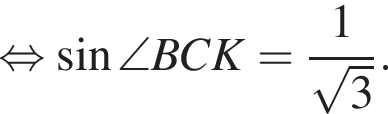
Тогда: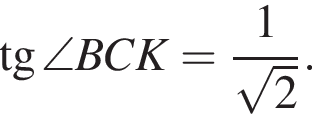

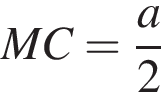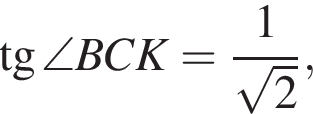Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник PMC, в ко­то­ром и тогда 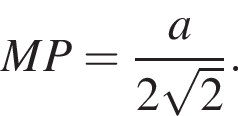Так как тре­уголь­ник ABC рав­но­сто­рон­ний, то H  — центр тре­уголь­ни­ка, от­ку­да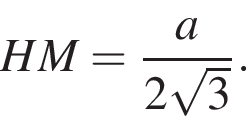

Из тре­уголь­ни­ка MHP по тео­ре­ме Пи­фа­го­ра 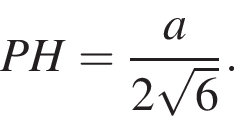По усло­вию вы­со­та пи­ра­ми­ды равна 3, тогда:

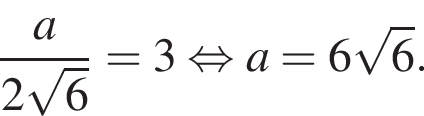
Вы­со­та ко­ну­са, опи­сан­но­го около пи­ра­ми­ды, равна вы­со­те, а ра­ди­ус ос­но­ва­ния ко­ну­са равен ра­ди­у­су опи­сан­но­го около тре­уголь­ни­ка ABC окруж­но­сти. Вос­поль­зу­ем­ся фор­му­лой объ­е­ма ко­ну­са, 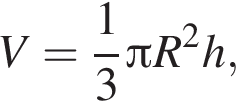где 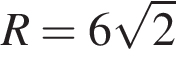и h  =  3:

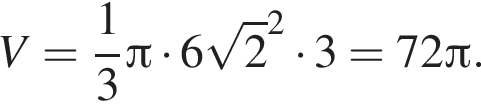
Ответ: 72π.