Задание № 550 

Классификатор алгебры: 3.2. Правильная треугольная пирамида, 3.19. Шар, 3.24. Комбинации многогранников и круглых тел
Методы алгебры: Использование подобия
Задания на 10 баллов
i
Каждое ребро треугольной пирамиды равно a. Найдите радиус вписанной в нее сферы.
Решение. Все грани этой пирамиды являются равными треугольниками. У правильной пирамиды центр описанной сферы лежит на высоте H = DO1, где O1 — центр основания. Тогда
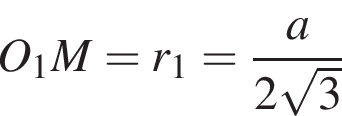 как радиус вписанной в основание окружности. Тогда
как радиус вписанной в основание окружности. Тогда 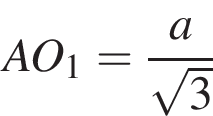 как радиус описанной около основания окружности. Имеем:
как радиус описанной около основания окружности. Имеем:
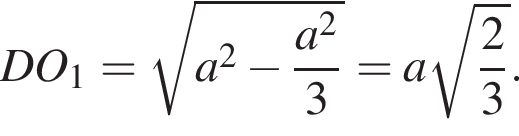
Сфера касается боковой грани правильной пирамиды в точке K, лежащей на апофеме, тогда OO1 = OK = r. Апофема 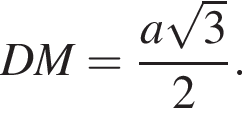
Из подобия треугольников OKD и AO1D имеем:
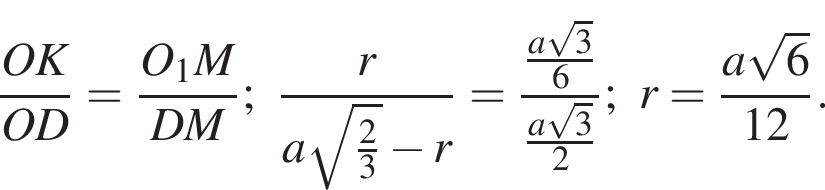
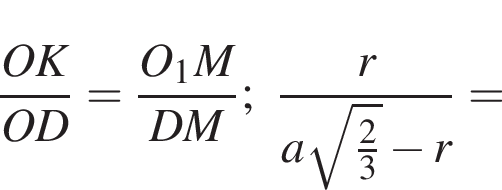
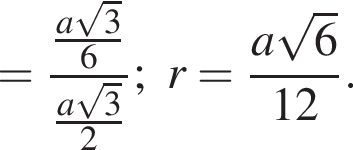
Ответ: ![]()
Ответ: 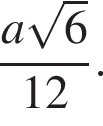
550
Классификатор алгебры: 3.2. Правильная треугольная пирамида, 3.19. Шар, 3.24. Комбинации многогранников и круглых тел
Методы алгебры: Использование подобия