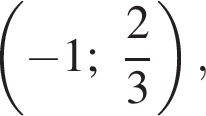РЕШУ ЦТ — математика–11

Задания

Задание № 697 Добавить в вариант

Классификатор алгебры: 14.4. Точки на графиках, пересечение, взаимное расположение графиков, 15.5. Касательная к графику функции, 15.8. Применение производной к исследованию функции

Задания на 7 баллов

К графику функции 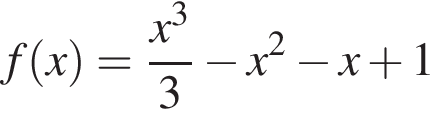$f левая круглая скобка x правая круглая скобка = дробь: числитель: x в кубе , знаменатель: 3 конец дроби минус x в квадрате минус x плюс 1$ проведены касательные, параллельные прямой 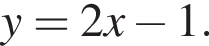$y=2x минус 1.$ Найдите координаты точек касания.

Решение. Возьмём производные от обеих функций:

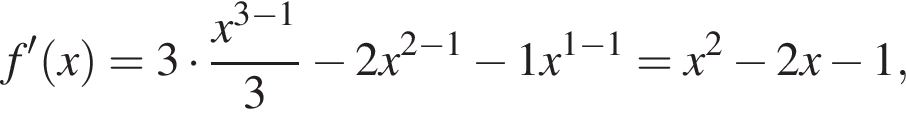
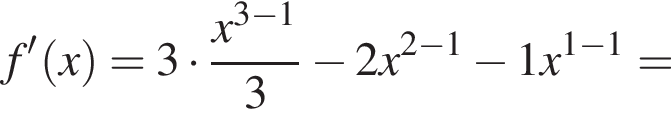
$f' левая круглая скобка x правая круглая скобка =3 умножить на дробь: числитель: x в степени левая круглая скобка 3 минус 1 правая круглая скобка , знаменатель: 3 конец дроби минус 2x в степени левая круглая скобка 2 минус 1 правая круглая скобка минус 1x в степени левая круглая скобка 1 минус 1 правая круглая скобка =x в квадрате минус 2x минус 1,$ $f' левая круглая скобка x правая круглая скобка =3 умножить на дробь: числитель: x в степени левая круглая скобка 3 минус 1 правая круглая скобка , знаменатель: 3 конец дроби минус 2x в степени левая круглая скобка 2 минус 1 правая круглая скобка минус 1x в степени левая круглая скобка 1 минус 1 правая круглая скобка =$
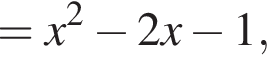
$=x в квадрате минус 2x минус 1,$ $f' левая круглая скобка x правая круглая скобка =$
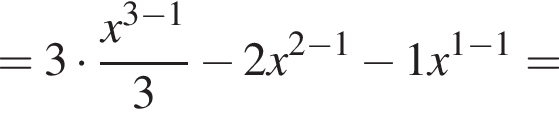
$=3 умножить на дробь: числитель: x в степени левая круглая скобка 3 минус 1 правая круглая скобка , знаменатель: 3 конец дроби минус 2x в степени левая круглая скобка 2 минус 1 правая круглая скобка минус 1x в степени левая круглая скобка 1 минус 1 правая круглая скобка =$
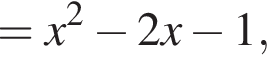
$=x в квадрате минус 2x минус 1,$

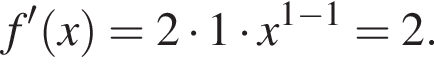
$f' левая круглая скобка x правая круглая скобка =2 умножить на 1 умножить на x в степени левая круглая скобка 1 минус 1 правая круглая скобка =2.$

Значение производной в точке касания равно угловому коэффициенту касательной. Решим квадратное уравнение, чтобы найти абсциссы точек касания:

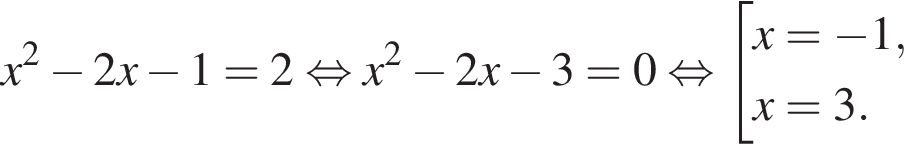
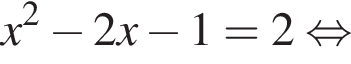
$x в квадрате минус 2x минус 1=2 равносильно x в квадрате минус 2x минус 3=0 равносильно совокупность выражений x= минус 1,x=3. конец совокупности .$ $x в квадрате минус 2x минус 1=2 равносильно$
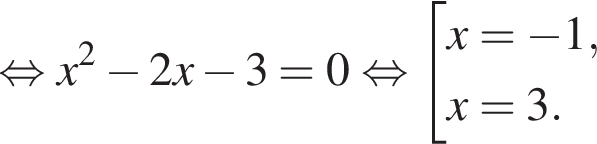
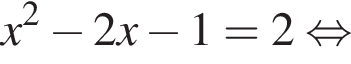
$равносильно x в квадрате минус 2x минус 3=0 равносильно совокупность выражений x= минус 1,x=3. конец совокупности .$ $x в квадрате минус 2x минус 1=2 равносильно$
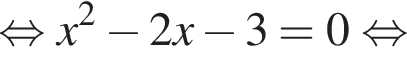
$равносильно x в квадрате минус 2x минус 3=0 равносильно$
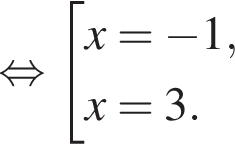
$равносильно совокупность выражений x= минус 1,x=3. конец совокупности .$

Подставим полученные значения в уравнение функции, чтобы найти ординаты точек пересечения

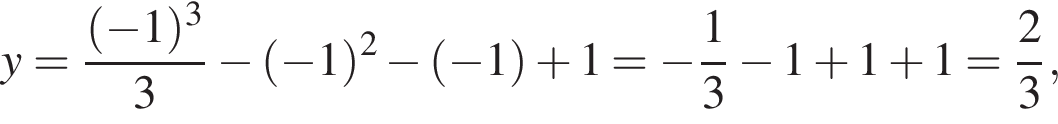
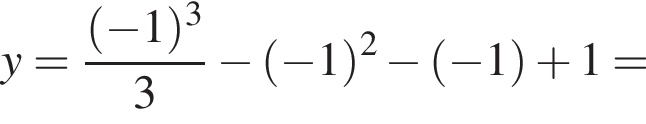
$y= дробь: числитель: левая круглая скобка минус 1 правая круглая скобка в кубе , знаменатель: 3 конец дроби минус левая круглая скобка минус 1 правая круглая скобка в квадрате минус левая круглая скобка минус 1 правая круглая скобка плюс 1= минус дробь: числитель: 1, знаменатель: 3 конец дроби минус 1 плюс 1 плюс 1= дробь: числитель: 2, знаменатель: 3 конец дроби ,$ $y= дробь: числитель: левая круглая скобка минус 1 правая круглая скобка в кубе , знаменатель: 3 конец дроби минус левая круглая скобка минус 1 правая круглая скобка в квадрате минус левая круглая скобка минус 1 правая круглая скобка плюс 1=$
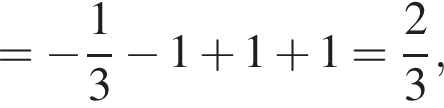
$= минус дробь: числитель: 1, знаменатель: 3 конец дроби минус 1 плюс 1 плюс 1= дробь: числитель: 2, знаменатель: 3 конец дроби ,$ $y=$
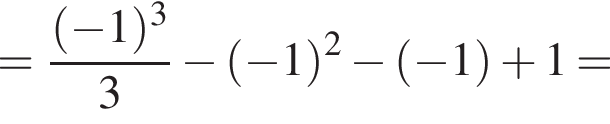
$= дробь: числитель: левая круглая скобка минус 1 правая круглая скобка в кубе , знаменатель: 3 конец дроби минус левая круглая скобка минус 1 правая круглая скобка в квадрате минус левая круглая скобка минус 1 правая круглая скобка плюс 1=$
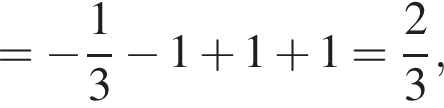
$= минус дробь: числитель: 1, знаменатель: 3 конец дроби минус 1 плюс 1 плюс 1= дробь: числитель: 2, знаменатель: 3 конец дроби ,$

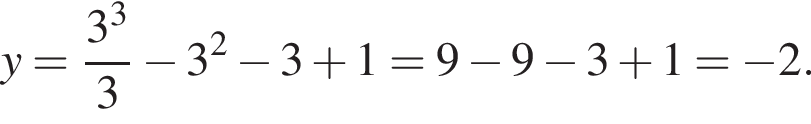
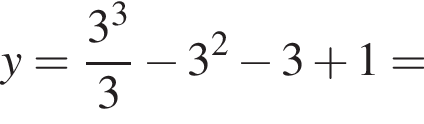
$y= дробь: числитель: 3 в кубе , знаменатель: 3 конец дроби минус 3 в квадрате минус 3 плюс 1=9 минус 9 минус 3 плюс 1= минус 2.$ $y= дробь: числитель: 3 в кубе , знаменатель: 3 конец дроби минус 3 в квадрате минус 3 плюс 1=$
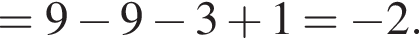
$=9 минус 9 минус 3 плюс 1= минус 2.$

Ответ: $левая круглая скобка минус 1; дробь: числитель: 2, знаменатель: 3 конец дроби правая круглая скобка ,$ $левая круглая скобка 3; минус 2 правая круглая скобка .$

697

$левая круглая скобка минус 1; дробь: числитель: 2, знаменатель: 3 конец дроби правая круглая скобка ,$ $левая круглая скобка 3; минус 2 правая круглая скобка .$

Ключ

№ п/п	№ задания	Ответ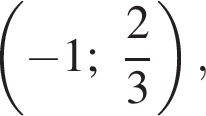
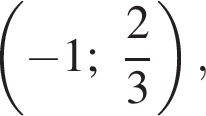
1	697	$левая круглая скобка минус 1; дробь: числитель: 2, знаменатель: 3 конец дроби правая круглая скобка ,$ $левая круглая скобка 3; минус 2 правая круглая скобка .$