РЕШУ ЦТ — математика–11

Задания

Задание № 827 Добавить в вариант

Классификатор алгебры: 3.10. Правильная треугольная призма, 3.19. Шар, 3.24. Комбинации многогранников и круглых тел, 4.1. Площадь поверхности многогранников

Задания на 10 баллов

Найдите полную поверхность правильной треугольной призмы, вписанной в шар радиуса 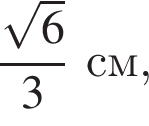$дробь: числитель: корень из: начало аргумента: 6 конец аргумента , знаменатель: 3 конец дроби см,$ которая имеет наибольшую боковую поверхность.

Решение. Пусть ABCA₁B₁C₁  — правильная треугольная призма, M и M₁  — центры ее оснований, O  — середина отрезка MM₁. Поскольку треугольники MOA, MOB, ... MOC1 равны по двум катетам, точка O равноудалена от всех вершин призмы и потому является ее центром описанного шара.

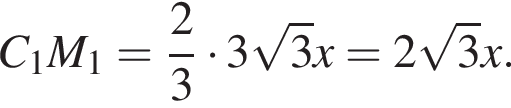Обозначим длину ребра основания призмы за 6x, тогда высота в основании равна $3 корень из: начало аргумента: 3 конец аргумента x,$ а $C_1M_1= дробь: числитель: 2, знаменатель: 3 конец дроби умножить на 3 корень из: начало аргумента: 3 конец аргумента x=2 корень из: начало аргумента: 3 конец аргумента x.$ Из треугольника C₁M₁O находим

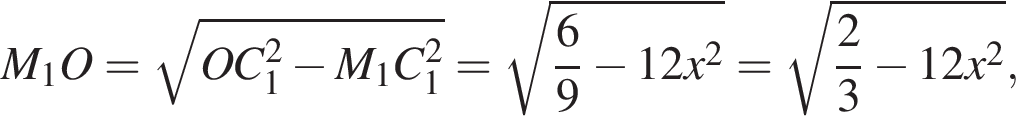
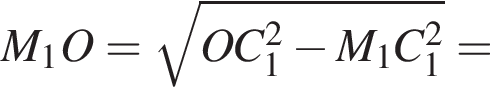
$M_1O= корень из: начало аргумента: OC_1 в квадрате минус M_1C_1 в квадрате конец аргумента = корень из: начало аргумента: дробь: числитель: 6, знаменатель: 9 конец дроби минус 12x в квадрате конец аргумента = корень из: начало аргумента: дробь: числитель: 2, знаменатель: 3 конец дроби минус 12x в квадрате конец аргумента ,$ $M_1O= корень из: начало аргумента: OC_1 в квадрате минус M_1C_1 в квадрате конец аргумента =$
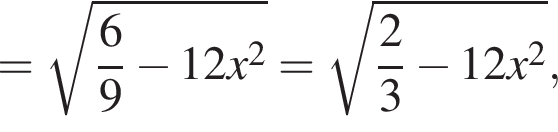
$= корень из: начало аргумента: дробь: числитель: 6, знаменатель: 9 конец дроби минус 12x в квадрате конец аргумента = корень из: начало аргумента: дробь: числитель: 2, знаменатель: 3 конец дроби минус 12x в квадрате конец аргумента ,$

поэтому высота призмы равна 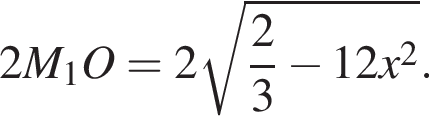$2M_1O=2 корень из: начало аргумента: дробь: числитель: 2, знаменатель: 3 конец дроби минус 12x в квадрате конец аргумента .$

Значит площадь ее боковой поверхности равна

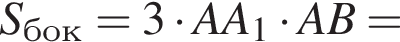
$S_бок = 3 умножить на AA_1 умножить на AB=$
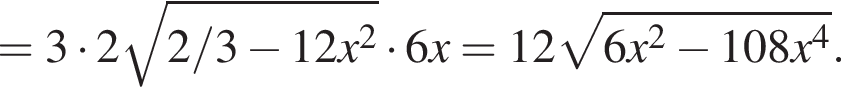
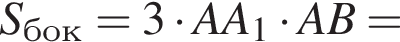
$=3 умножить на 2 корень из: начало аргумента: 2/3 минус 12x в квадрате конец аргумента умножить на 6x=12 корень из: начало аргумента: 6x в квадрате минус 108x в степени 4 конец аргумента .$ $S_бок = 3 умножить на AA_1 умножить на AB=$
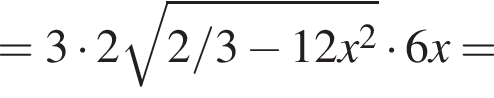
$=3 умножить на 2 корень из: начало аргумента: 2/3 минус 12x в квадрате конец аргумента умножить на 6x=$
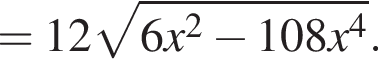
$=12 корень из: начало аргумента: 6x в квадрате минус 108x в степени 4 конец аргумента .$

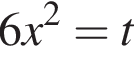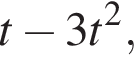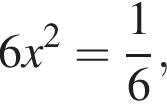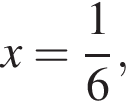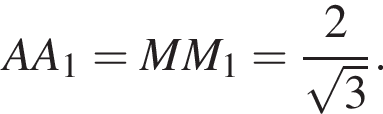
Найдем максимум этого выражения. Обозначая временно $6x в квадрате =t$ получим под корнем $t минус 3t в квадрате ,$ что достигает максимума при $t= дробь: числитель: 1, знаменатель: 6 конец дроби$ (вершина параболы). Значит, $6x в квадрате = дробь: числитель: 1, знаменатель: 6 конец дроби ,$ откуда $x= дробь: числитель: 1, знаменатель: 6 конец дроби ,$ AB  =  1 и $AA_1=MM_1= дробь: числитель: 2, знаменатель: корень из: начало аргумента: 3 конец аргумента конец дроби .$

Площадь полной поверхности этой призмы равна

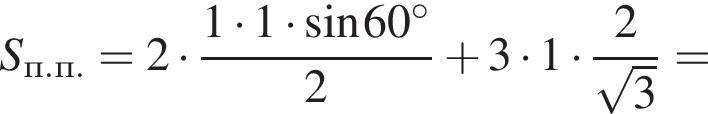
$S_п.п.=2 умножить на дробь: числитель: 1 умножить на 1 умножить на синус 60 градусов , знаменатель: 2 конец дроби плюс 3 умножить на 1 умножить на дробь: числитель: 2, знаменатель: корень из: начало аргумента: 3 конец аргумента конец дроби =$
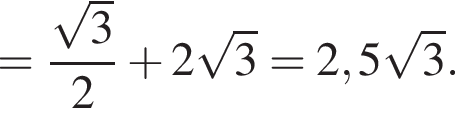
$= дробь: числитель: корень из: начало аргумента: 3 конец аргумента , знаменатель: 2 конец дроби плюс 2 корень из: начало аргумента: 3 конец аргумента =2,5 корень из: начало аргумента: 3 конец аргумента .$ $S_п.п.=$
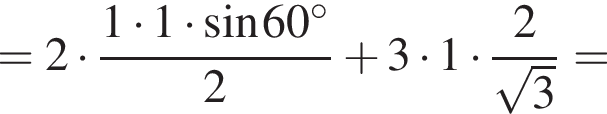
$=2 умножить на дробь: числитель: 1 умножить на 1 умножить на синус 60 градусов , знаменатель: 2 конец дроби плюс 3 умножить на 1 умножить на дробь: числитель: 2, знаменатель: корень из: начало аргумента: 3 конец аргумента конец дроби =$
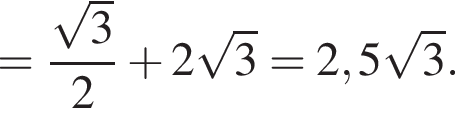
$= дробь: числитель: корень из: начало аргумента: 3 конец аргумента , знаменатель: 2 конец дроби плюс 2 корень из: начало аргумента: 3 конец аргумента =2,5 корень из: начало аргумента: 3 конец аргумента .$

Ответ: $2,5 корень из 3 .$

827

$2,5 корень из 3 .$

Ключ

№ п/п	№ задания	Ответ
1	827	$2,5 корень из 3 .$