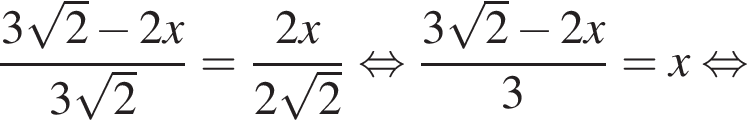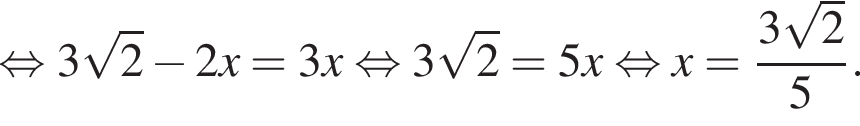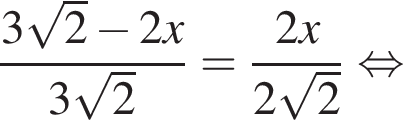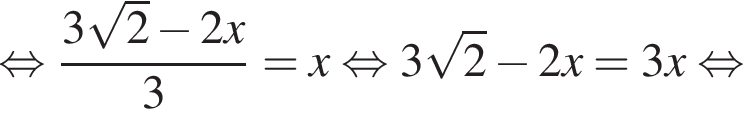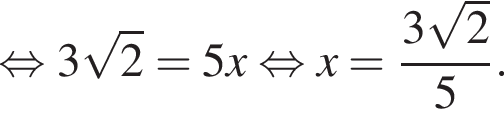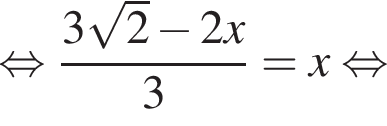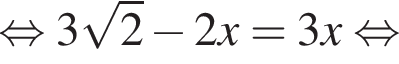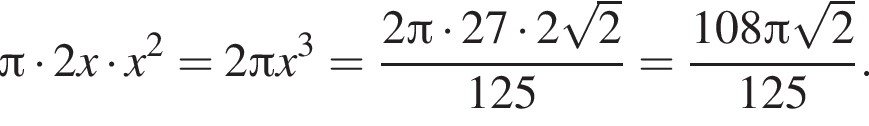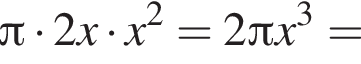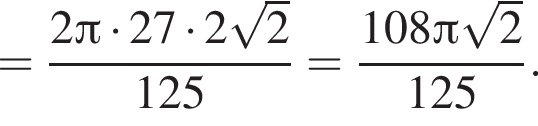В правильную четырехугольную пирамиду вписан цилиндр, осевым сечением которого является квадрат, так, что одно основание цилиндра лежит на основании пирамиды, а другое основание цилиндра касается боковых граней пирамиды. Найдите объем цилиндра, если высота пирамиды равна 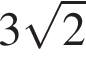 см, а сторона основания пирамиды равна
см, а сторона основания пирамиды равна  см.
см.
Решение. В треугольник TPM вписан квадрат 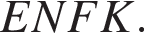 Пусть его сторона равна
Пусть его сторона равна 
Тогда имеем
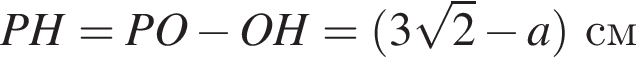
и 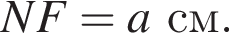 Рассмотрим треугольники PTM и PNF. В них
Рассмотрим треугольники PTM и PNF. В них 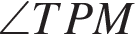 — общий, а
— общий, а  как соответственные углы при параллельных прямых NF и TM (PT — секущая). Тогда эти треугольники подобны до двум углам, следовательно:
как соответственные углы при параллельных прямых NF и TM (PT — секущая). Тогда эти треугольники подобны до двум углам, следовательно:
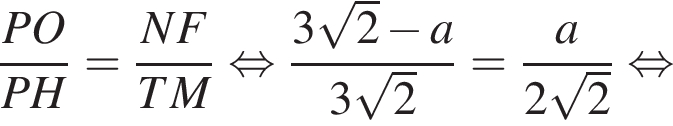
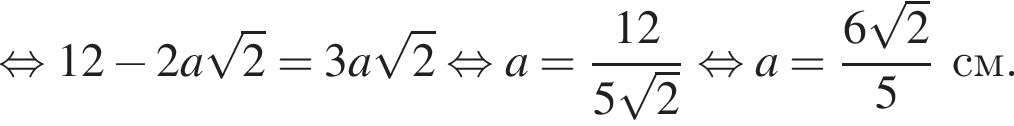
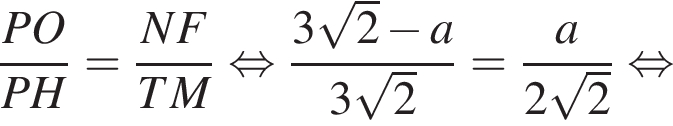
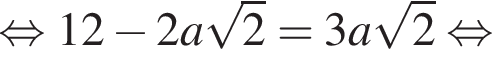
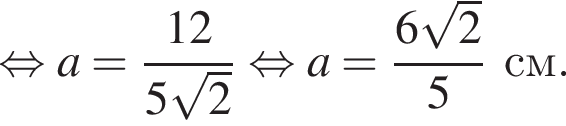
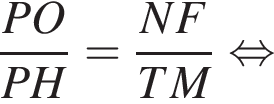
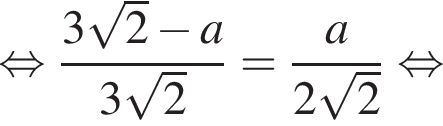
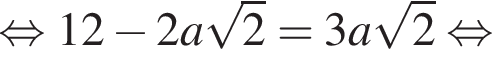
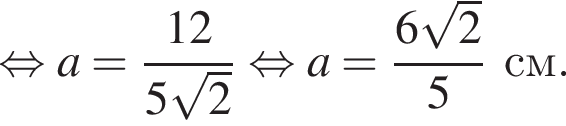
Найдем объём цилиндра:
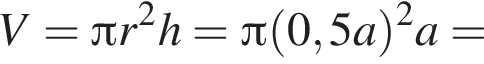
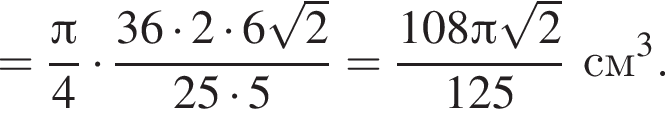
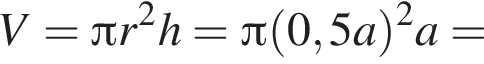
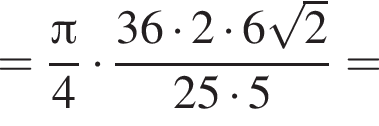
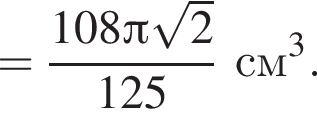
Ответ: 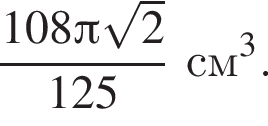
Приведем другое решение.
Заметим, что ось цилиндра совпадает с высотой пирамиды, а точки касания верхнего основания с боковыми гранями лежат на апофемах (из симметрии пирамиды). Пусть T и M — середины ребер при основании, N и F — точки касания верхнего основания цилиндра с отрезками PT и PM соответственно, N1 и F1 — вторые концы образующих цилиндра с концами N и F соответственно. Рассмотрим сечение плоскостью PMT, все указанные точки лежат в этом сечении. Пусть, далее, радиус основания цилиндра равен r, тогда 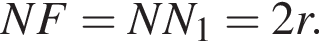
Поскольку  треугольники PNF и PMT подобны, поэтому их высоты относятся так же, как их стороны. При этом
треугольники PNF и PMT подобны, поэтому их высоты относятся так же, как их стороны. При этом 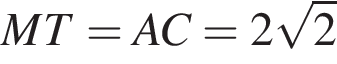 и
и  Значит,
Значит,
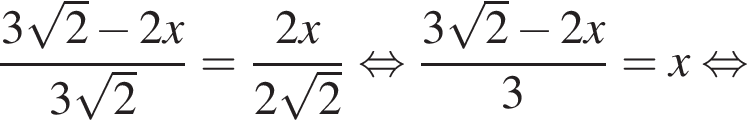
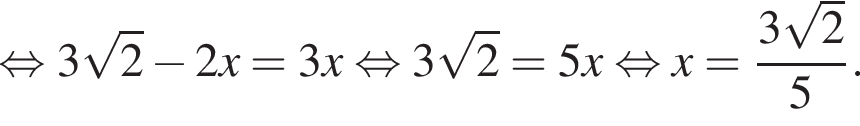
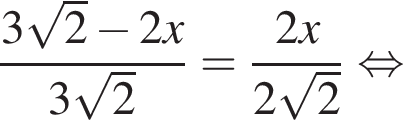
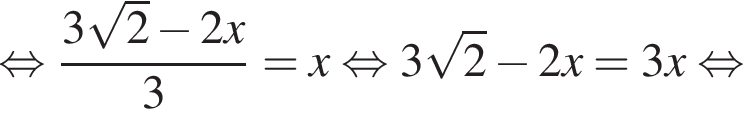
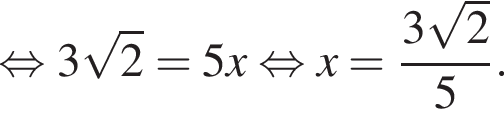
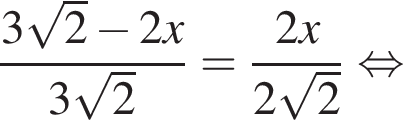
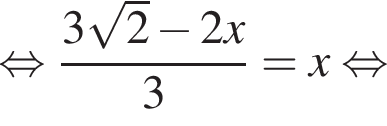
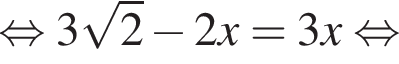
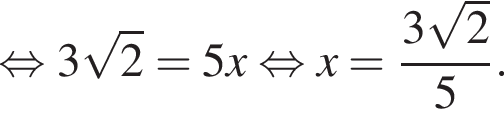
Наконец, объем цилиндра равен
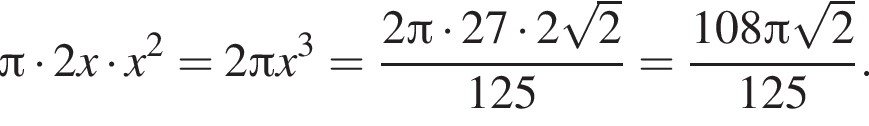
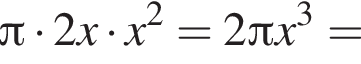
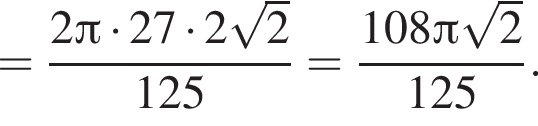
![]() см, а сторона основания пирамиды равна
см, а сторона основания пирамиды равна ![]() см.
см.
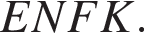 Пусть его сторона равна
Пусть его сторона равна 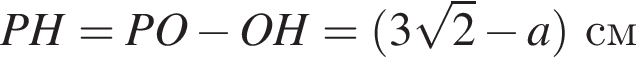
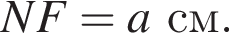 Рассмотрим треугольники PTM и PNF. В них
Рассмотрим треугольники PTM и PNF. В них 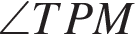 — общий, а
— общий, а  как соответственные углы при параллельных прямых NF и TM (PT — секущая). Тогда эти треугольники подобны до двум углам, следовательно:
как соответственные углы при параллельных прямых NF и TM (PT — секущая). Тогда эти треугольники подобны до двум углам, следовательно: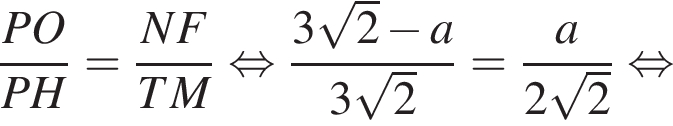
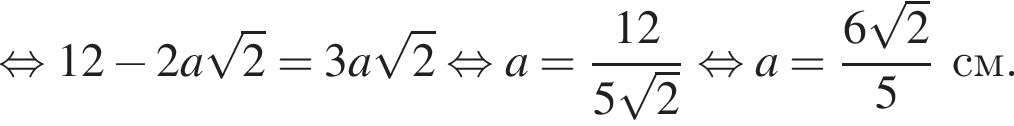
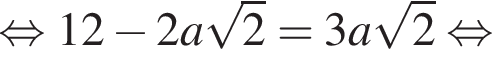
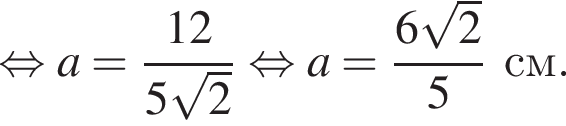
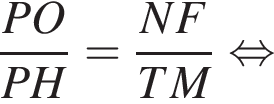
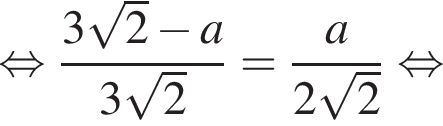
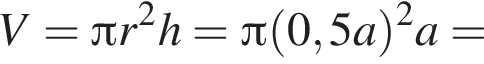
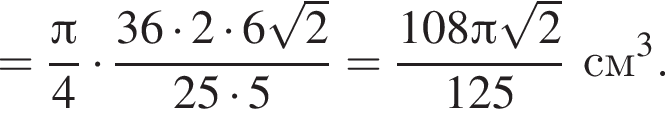
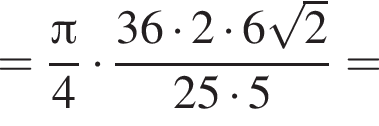
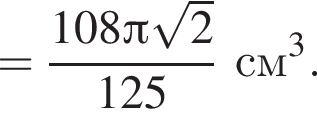
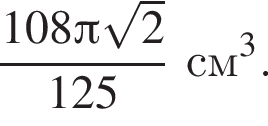
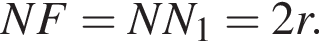
 треугольники PNF и PMT подобны, поэтому их высоты относятся так же, как их стороны. При этом
треугольники PNF и PMT подобны, поэтому их высоты относятся так же, как их стороны. При этом 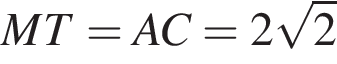 и
и  Значит,
Значит,