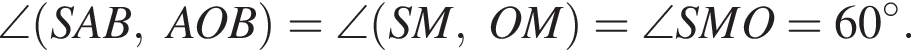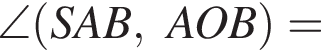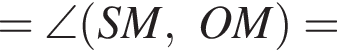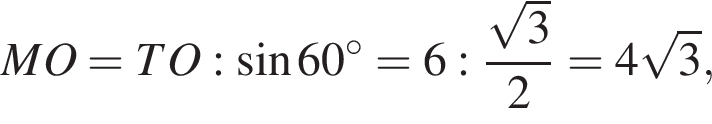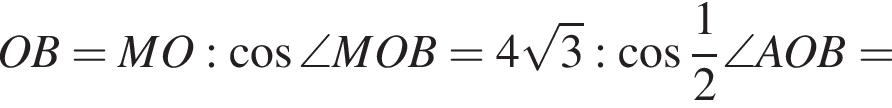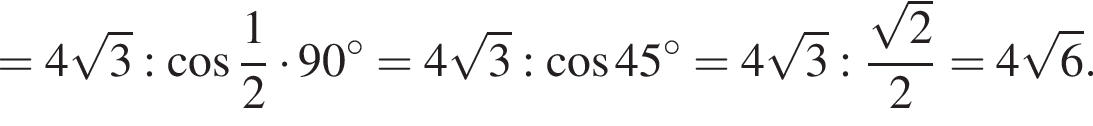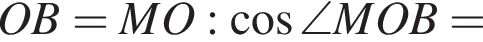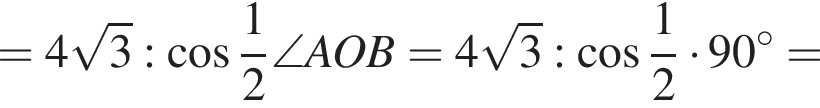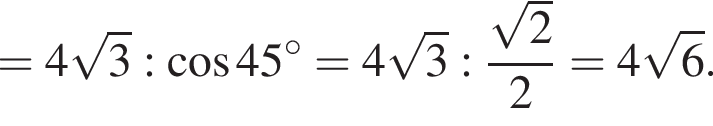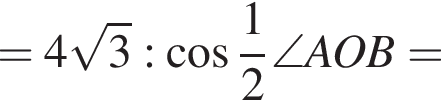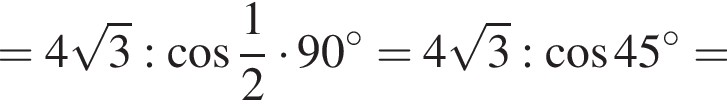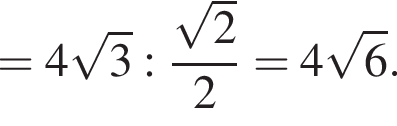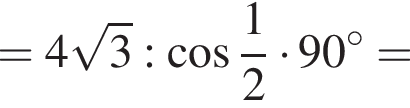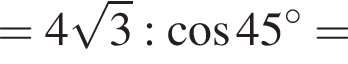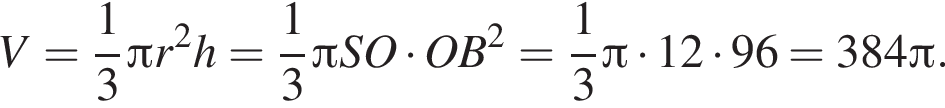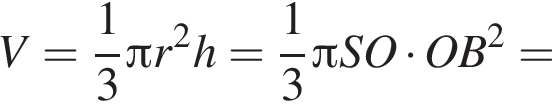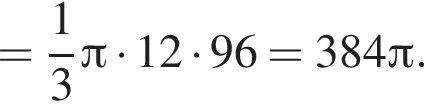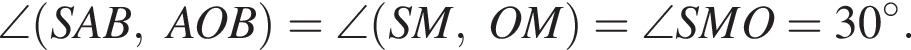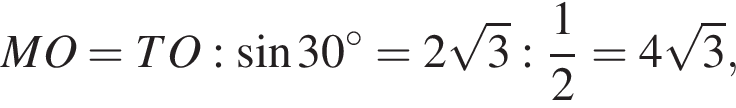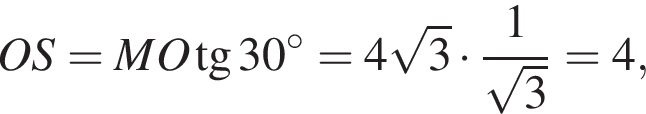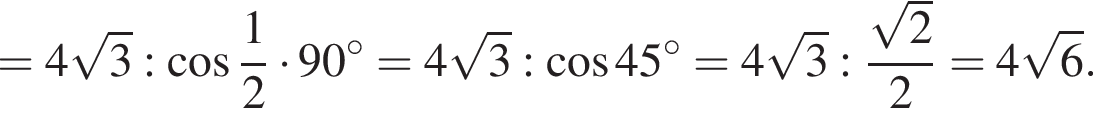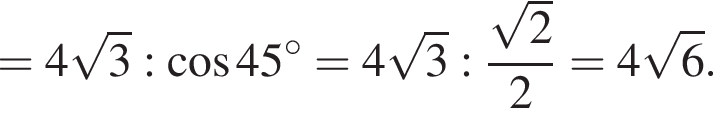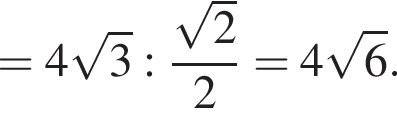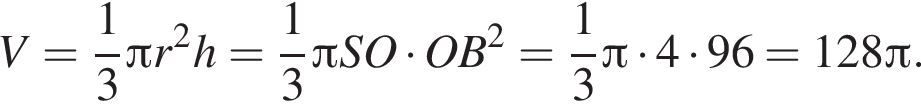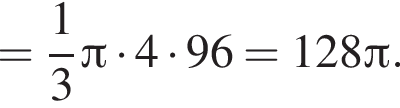Через вершину конуса под углом 60° к основанию проведена плоскость, отсекающая от окружности основания дугу в 90. Найдите объем конуса, если расстояние от центра основания до плоскости сечения равно 6 см.
Решение. Обозначим вершину конуса за S, центр его основания за O, концы указанной дуги за A и B, середину хорды AB за M и основание перпендикуляра, опущенного из O на SM за T.
Заметим, что OM перпендикулярна AB, так как является медианой равнобедренного треугольника AOB, и OS перпендикулярна AB, следовательно, и плоскость MOS перпендикулярна AB, поэтому OT перпендикулярна AB.
Значит, OT перпендикулярно к двум пересекающимся прямым AB и MS в плоскости ABS, поэтому OT и есть расстояние от центра основания до плоскости сечения.
Далее, по теореме о трех перпендикулярах SM перпендикулярна AB, поскольку его проекция на плоскость основания это OM, перпендикулярная AB. Тогда
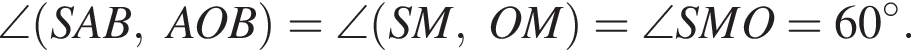


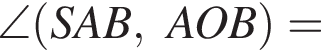
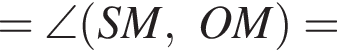

Тогда:
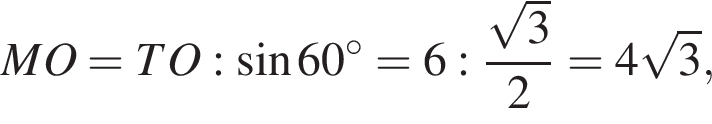

откуда
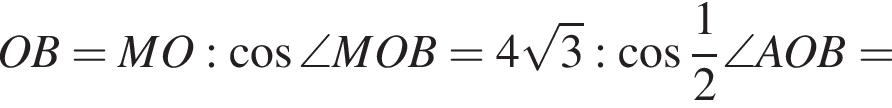
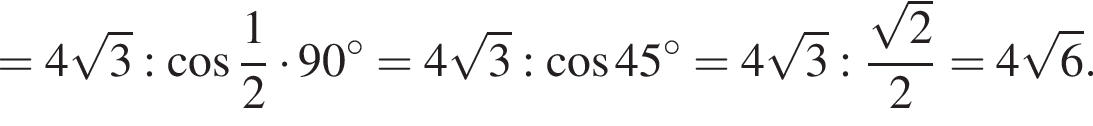
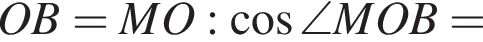
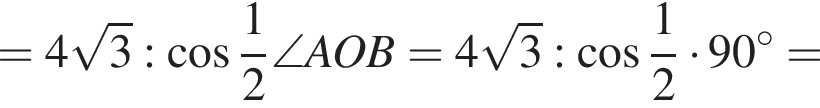
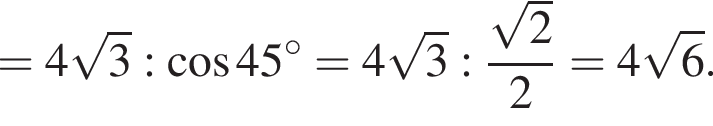
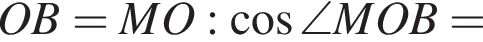
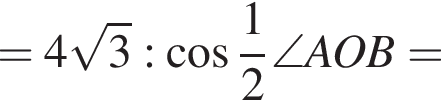
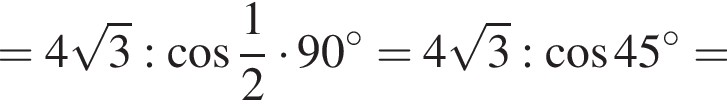
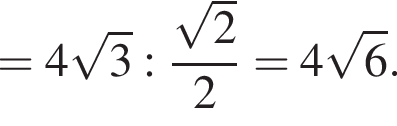
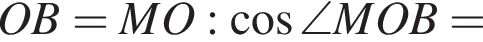
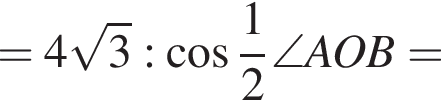
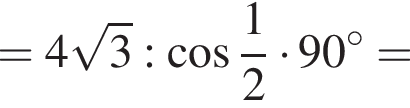
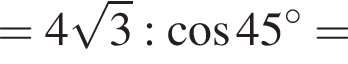
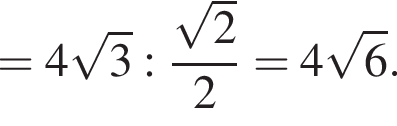
Следовательно, объем конуса равен:
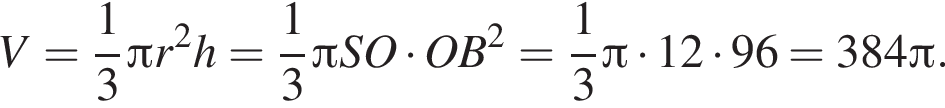
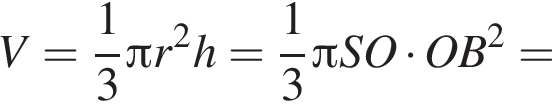
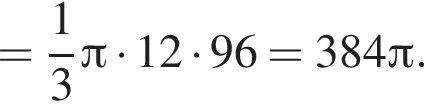
Ответ: 
Ответ: 
![]() см.
см.