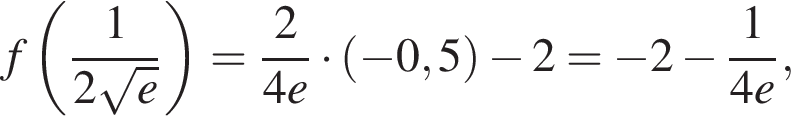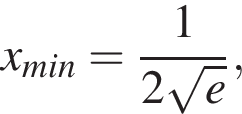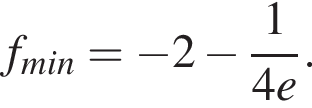1. Задание № 1086 

Классификатор алгебры: 13.3. Монотонность и экстремумы функции , 13.4. Наибольшее и наименьшее значение функции
Задания на 9 баллов
i
Найдите промежутки монотонности, точки экстремума и экстремумы функции 
Решение. Возьмем производную данной функции:
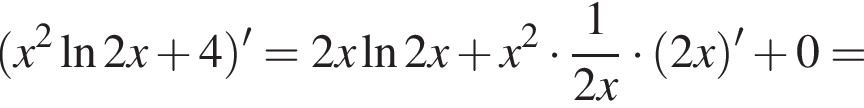
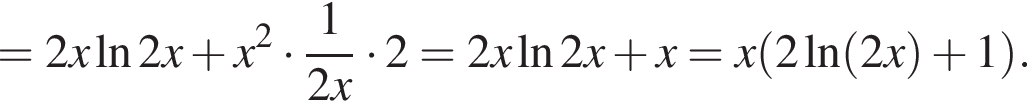
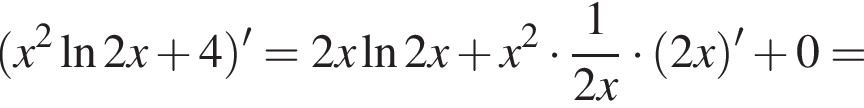
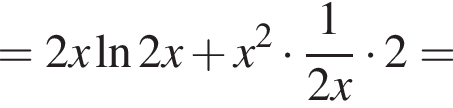
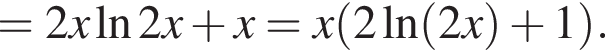
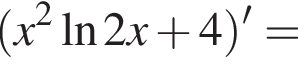
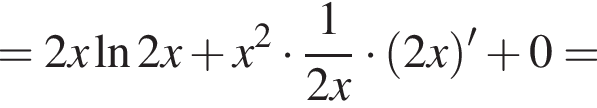
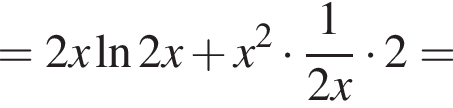
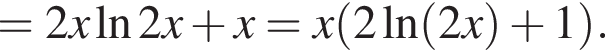
Очевидно, что первый множитель положителен, иначе изначальная функция не определена. Исследуем теперь знак выражения 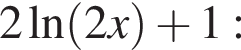
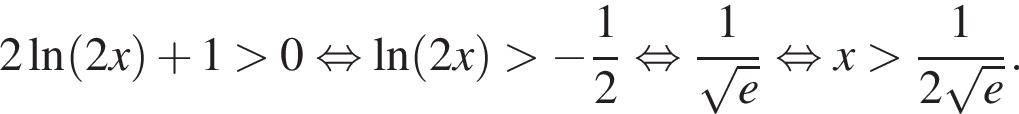
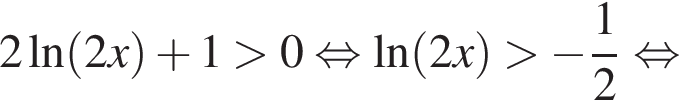
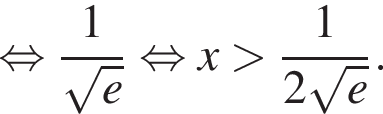

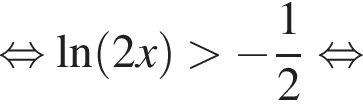
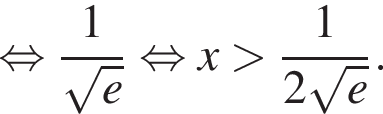
Отсюда видно, что при 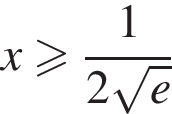 функция возрастает, при
функция возрастает, при 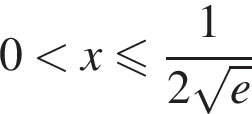 убывает, при
убывает, при 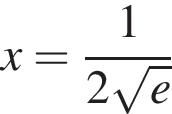 имеет минимум, причем
имеет минимум, причем
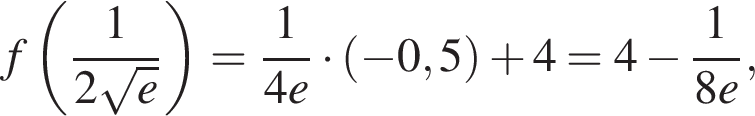
а при ![]() вообще не определена.
вообще не определена.
Ответ: при 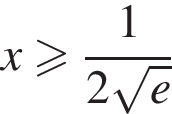 функция возрастает, при
функция возрастает, при 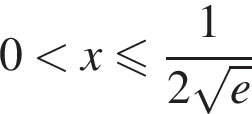 убывает,
убывает, 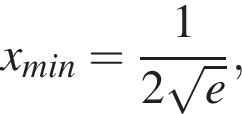
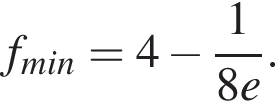
Ответ: при 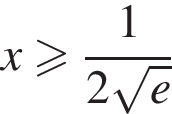 функция возрастает, при
функция возрастает, при 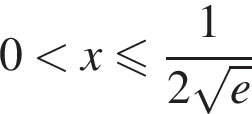 убывает,
убывает, 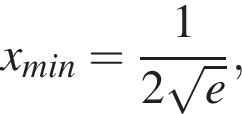
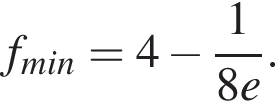
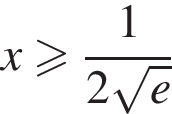 функция возрастает, при
функция возрастает, при 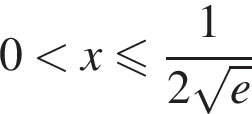 убывает,
убывает, 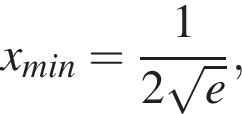
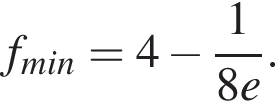
1086
при 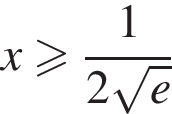 функция возрастает, при
функция возрастает, при 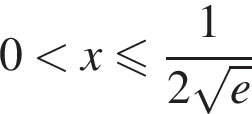 убывает,
убывает, 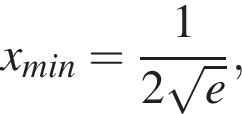
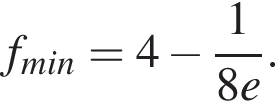
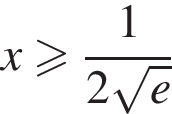 функция возрастает, при
функция возрастает, при 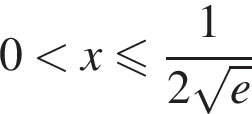 убывает,
убывает, 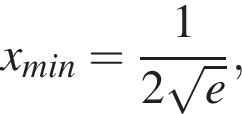
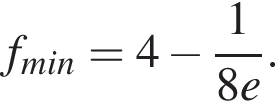
Классификатор алгебры: 13.3. Монотонность и экстремумы функции , 13.4. Наибольшее и наименьшее значение функции
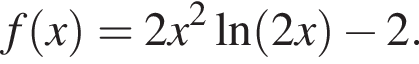
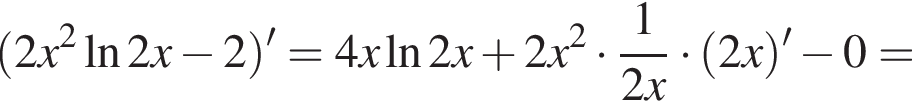
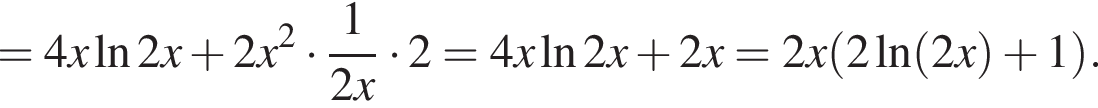
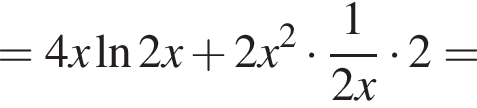

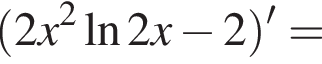
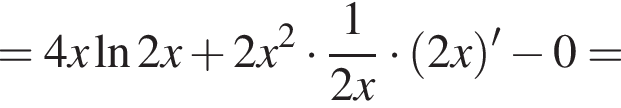


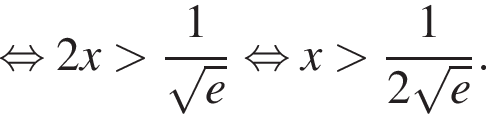
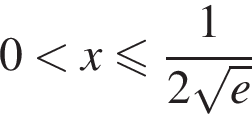 убывает, при
убывает, при 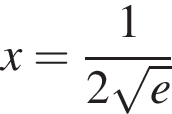 имеет минимум, причем
имеет минимум, причем