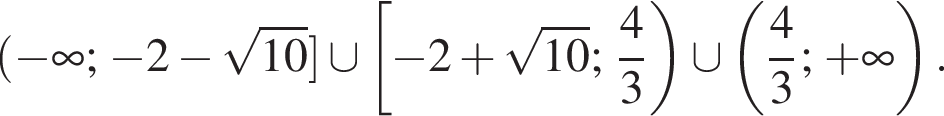1. Задание № 967 
Классификатор алгебры: 5.2. Неравенства первой и второй степени относительно логарифмических функций
Задания на 10 баллов
i
Решите неравенство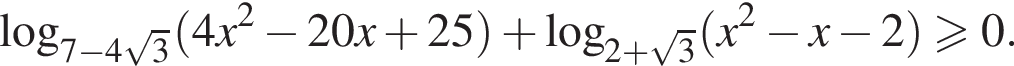 
Решение. Сразу заметим, что
и 
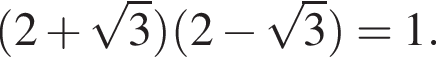
Пусть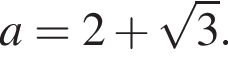 
Далее, должны выполняться условия:
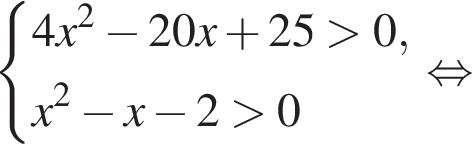
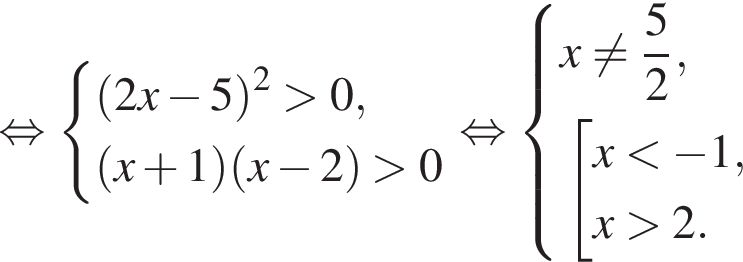
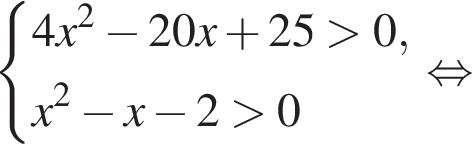
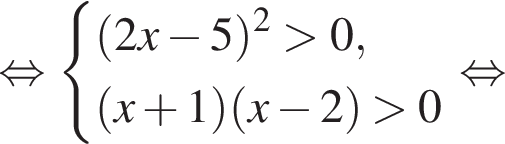
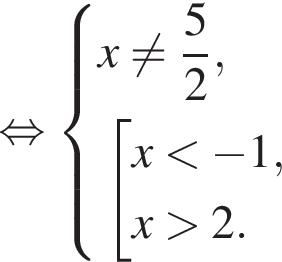
Итак, ОДЗ уравнения: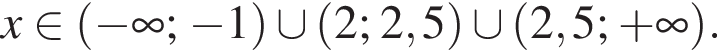 
Преобразуем теперь уравнение:
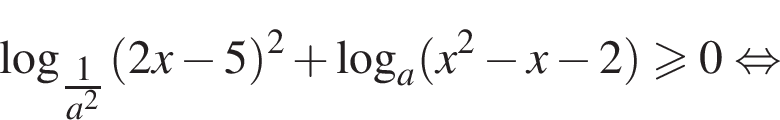
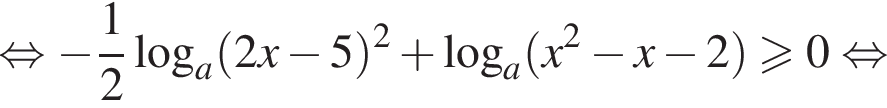
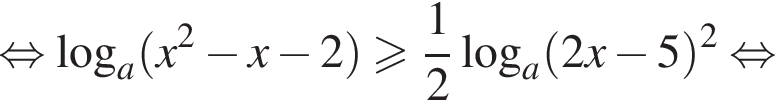
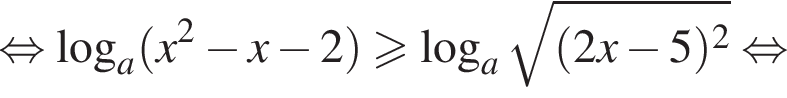
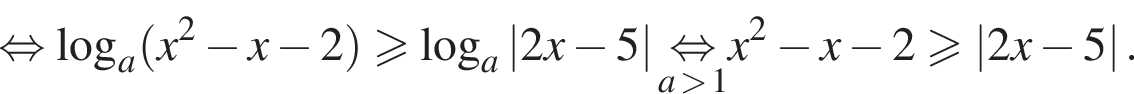
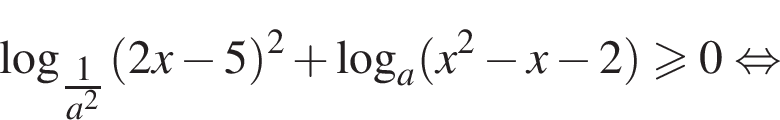
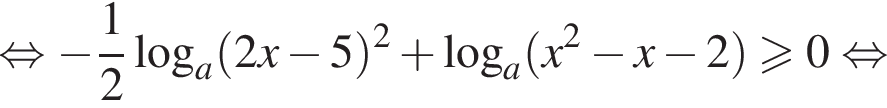
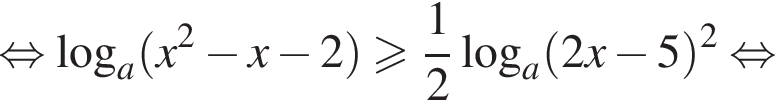
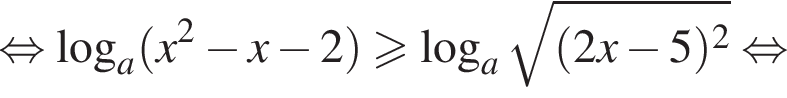
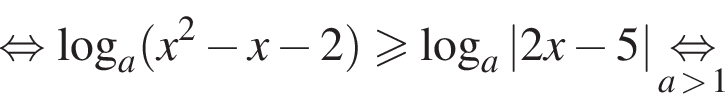
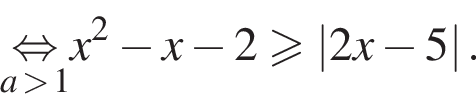
Разберем теперь два случая.
При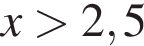 
неравенство принимает вид:
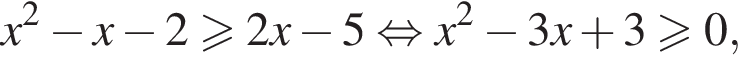
что верно при всех x, поскольку дискриминант уравнения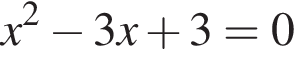 
отрицателен.
При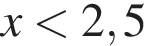 
неравенство принимает вид:
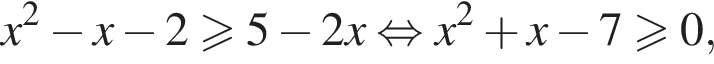
что верно при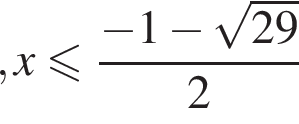 
или 
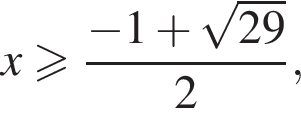поскольку корни уравнения 
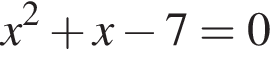равны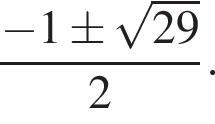 
Заметим, что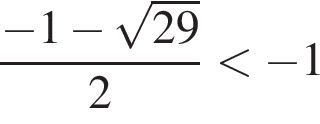 
и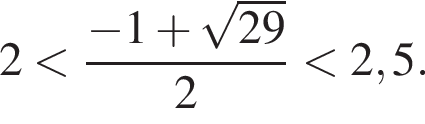 
Поэтому учитывать ОДЗ не потребуется: случай 
мы сразу даже разбирать не стали.
Осталось выбрать из первого случая 
а из второго 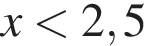и объединить полученные ответы.
Ответ: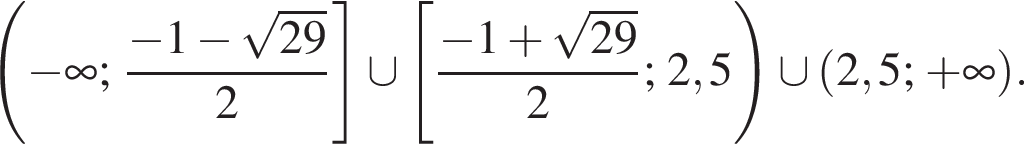 
Ответ: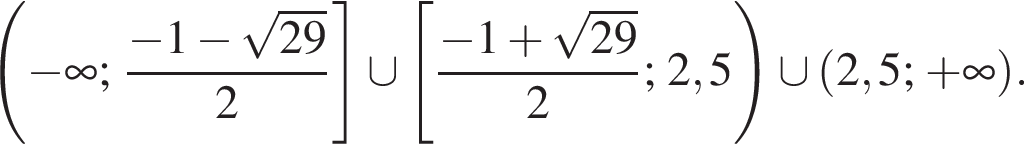
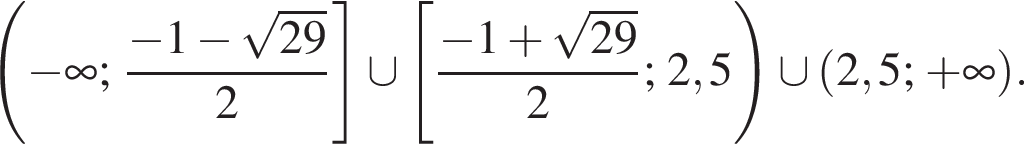
967
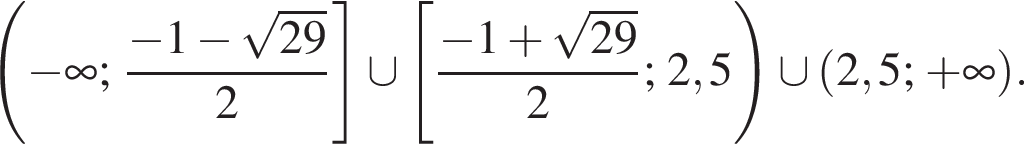
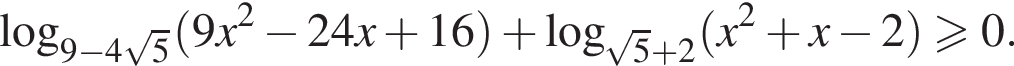
и 
неравенство принимает вид:
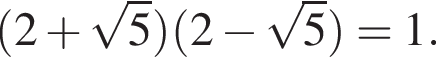
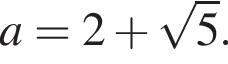
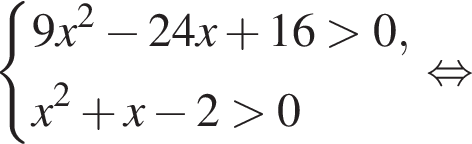
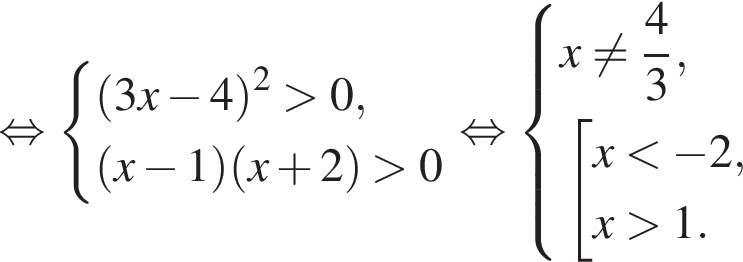
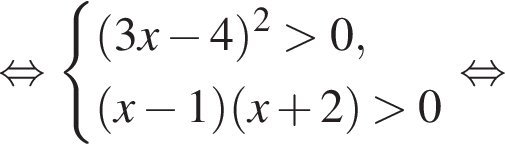
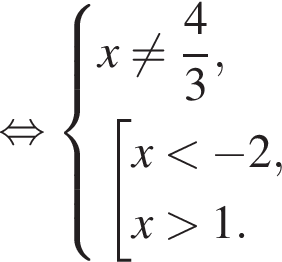
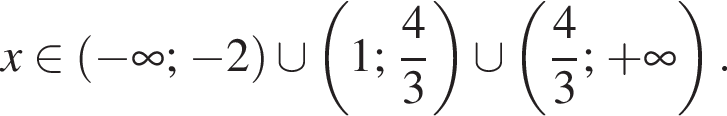
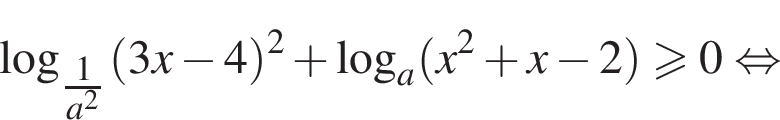
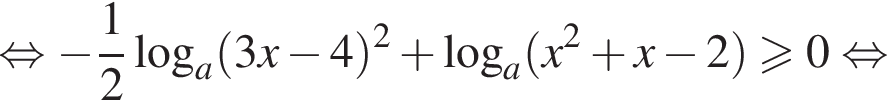
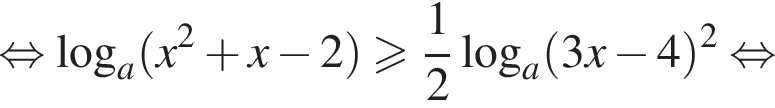
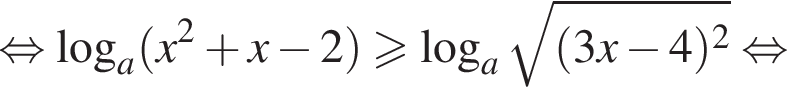
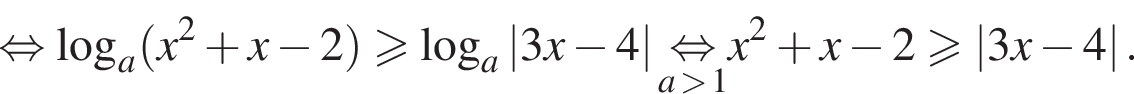
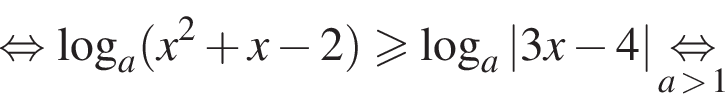
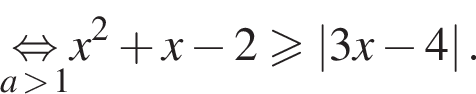
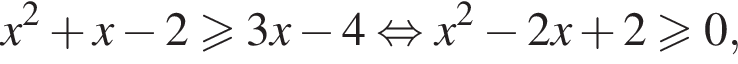
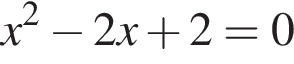отрицателен.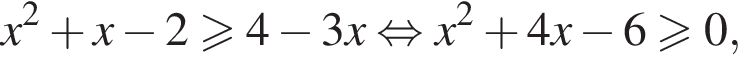
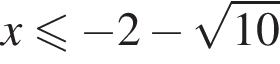неравенство принимает вид:
или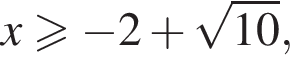 
поскольку корни уравнения 
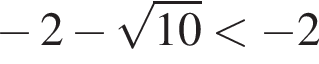и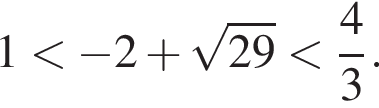 
Поэтому учитывать ОДЗ не потребуется: случай 
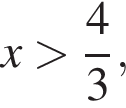а из второго 