Задание № 1366 

Классификатор алгебры: 13.3. Монотонность и экстремумы функции , 13.4. Наибольшее и наименьшее значение функции
Задания на 9 баллов
i
Исследуйте функцию 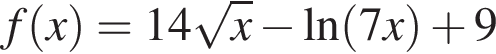 на монотонность и экстремумы.
на монотонность и экстремумы.
Решение. Чтобы исследовать функцию на монотонность и экстремумы, возьмем производную данной функции, определенной при ![]() Получим:
Получим:
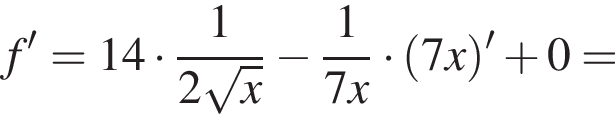
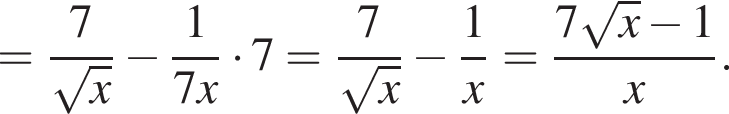
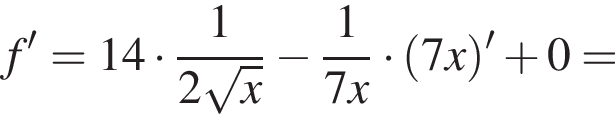
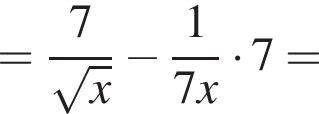
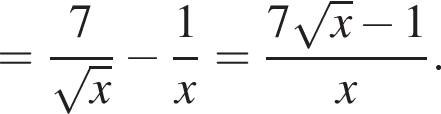
![]()
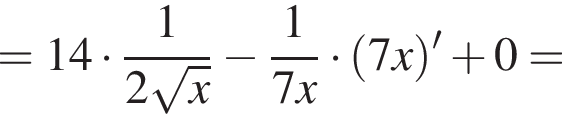
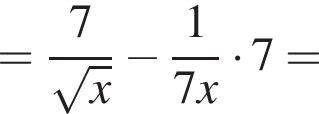
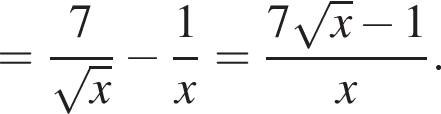
Знаменатель всегда положителен, а числитель положителен при условии 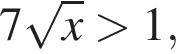 то есть
то есть 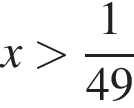 и отрицателен при
и отрицателен при 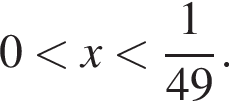 Значит, изначальная функция возрастает на промежутке
Значит, изначальная функция возрастает на промежутке 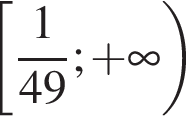 и убывает на промежутке
и убывает на промежутке 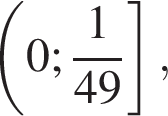 поэтому
поэтому 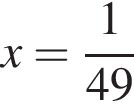 — точка минимума, причём
— точка минимума, причём
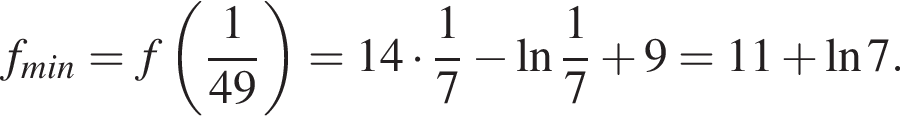
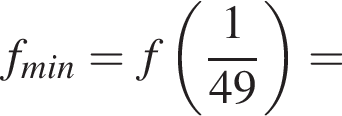
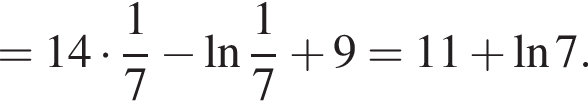
Ответ: функция убывает на промежутке 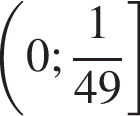 и возрастает на промежутке
и возрастает на промежутке 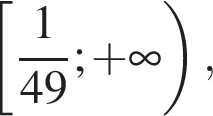
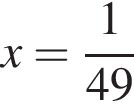 — точка минимума,
— точка минимума, 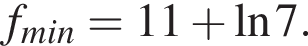
Ответ: функция убывает на промежутке 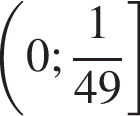 и возрастает на промежутке
и возрастает на промежутке 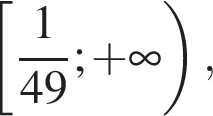
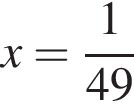 — точка минимума,
— точка минимума, 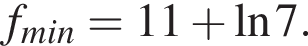
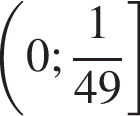 и возрастает на промежутке
и возрастает на промежутке 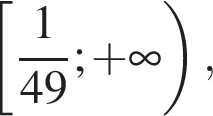
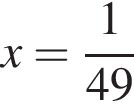 — точка минимума,
— точка минимума, 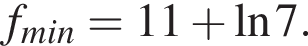
1366
функция убывает на промежутке 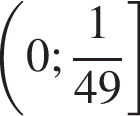 и возрастает на промежутке
и возрастает на промежутке 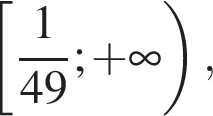
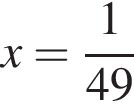 — точка минимума,
— точка минимума, 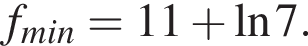
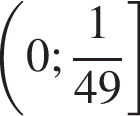 и возрастает на промежутке
и возрастает на промежутке 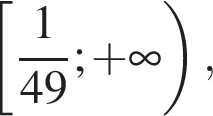
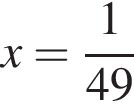 — точка минимума,
— точка минимума, 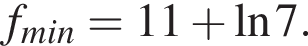
Классификатор алгебры: 13.3. Монотонность и экстремумы функции , 13.4. Наибольшее и наименьшее значение функции