РЕШУ ЦТ — математика–11

Задания

Задание № 586 Добавить в вариант

Классификатор алгебры: 3.10. Правильная треугольная призма, 3.19. Шар, 3.24. Комбинации многогранников и круглых тел

Задания на 6 баллов

Сфера радиусом $2 корень из: начало аргумента: 3 конец аргумента$ описана вокруг правильной треугольной призмы. Ребро основания призмы равно $2 корень из: начало аргумента: 3 конец аргумента .$ Найдите высоту призмы.

Решение. Введём обозначения, как показано на рисунке (см. рис). Отрезок A₁O  — радиус описанной вокруг призмы сферы, он равен $2 корень из 3 .$ Отрезок, соединяющий центры оснований призмы O₁O₂  — высота призмы. Отрезок OO₁ равен половине этой высоты (радиус вписанной в призму сферы). Найдём радиус описанной окружности треугольника A₁B₁C₁:

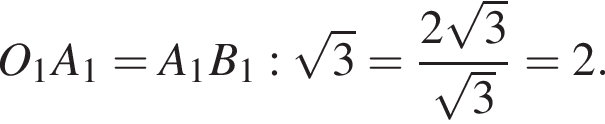
$O_1A_1 = A_1B_1 : корень из 3 = дробь: числитель: 2 корень из 3 , знаменатель: корень из 3 конец дроби = 2.$

По теореме Пифагора в прямоугольном треугольнике OO₁A₁:

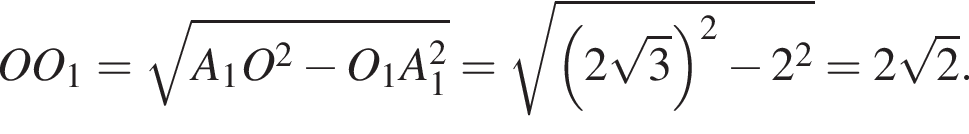
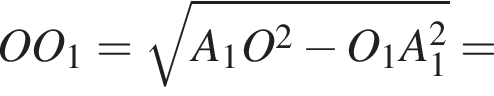
$OO_1= корень из: начало аргумента: A_1O в квадрате минус O_1A_1 в квадрате конец аргумента = корень из: начало аргумента: левая круглая скобка 2 корень из 3 правая круглая скобка в квадрате минус 2 в квадрате конец аргумента =2 корень из 2 .$ $OO_1= корень из: начало аргумента: A_1O в квадрате минус O_1A_1 в квадрате конец аргумента =$
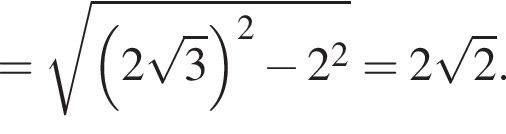
$= корень из: начало аргумента: левая круглая скобка 2 корень из 3 правая круглая скобка в квадрате минус 2 в квадрате конец аргумента =2 корень из 2 .$

Найдём высоту призмы:

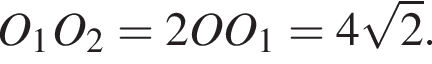
$O_1O_2 = 2OO_1 = 4 корень из 2 .$

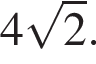
Ответ: $4 корень из 2 .$

586

$4 корень из 2 .$

Методы алгебры: Теорема Пифагора

Ключ

№ п/п	№ задания	Ответ
1	586	$4 корень из 2 .$