Укажите точку, через которую проходит график функции 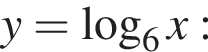
а) A (1; 6);
б) B (2; 36);
в) C (36; 2);
г) D (-6; -1).
Укажите точку, через которую проходит график функции 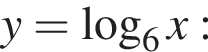
а) A (1; 6);
б) B (2; 36);
в) C (36; 2);
г) D (-6; -1).
Высота пирамиды равна 7 см, а основанием ее является прямоугольный треугольник с катетами 2 и 5 см. Объем пирамиды равен:
а) ![]() см3
см3
б) ![]() см3
см3
в) ![]() см3
см3
г) ![]() см3
см3
Решите уравнение 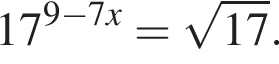
Решите неравенство 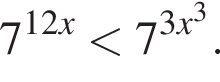
Вычислите ![]() если
если 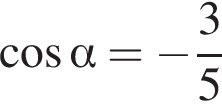 и
и 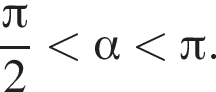
Стороны оснований правильной треугольной усеченной пирамиды равны 12 и 6 см, высота — 4 см. Через сторону большего основания и противоположную ей вершину меньшего основания проведена плоскость. Найдите площадь полученного сечения.
Решите уравнение 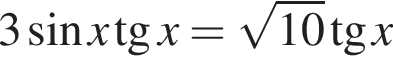 и найдите среднее арифметическое корней уравнения, принадлежащих промежутку
и найдите среднее арифметическое корней уравнения, принадлежащих промежутку 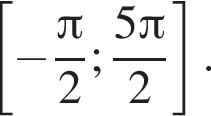
Решите систему уравнений 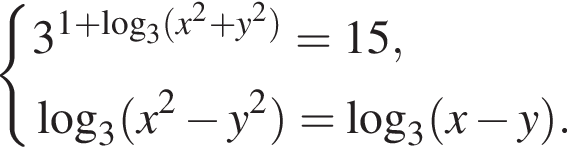
Вычислите: 
Куб, шар и цилиндр, осевым сечением которого является квадрат, имеют равные площади полных поверхностей. Найдите, какая из данных фигур имеет наибольший объем.