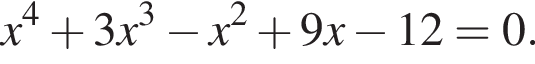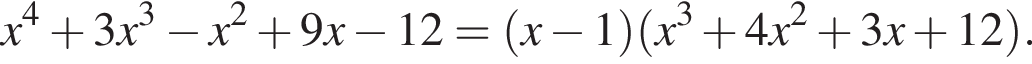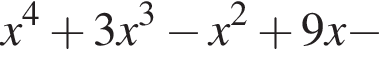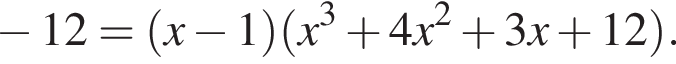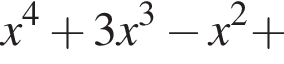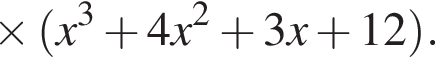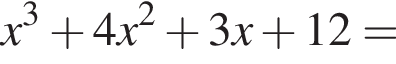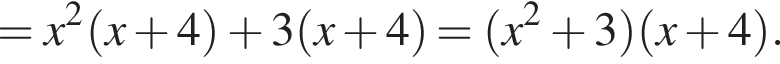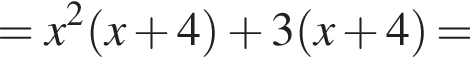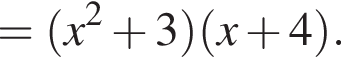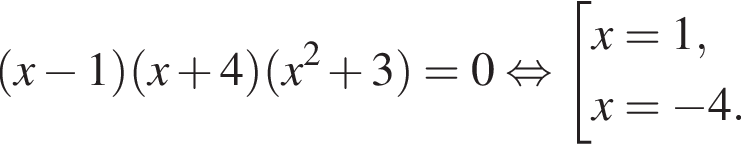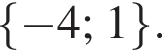1. Задание № 1205 

Классификатор алгебры: 3.7. Уравнения высших степеней
Методы алгебры: Группировка, разложение на множители
Задания на 8 баллов
i
Решите уравнение 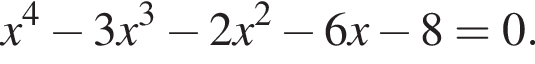
Решение. Подберем сначала целый корень данного уравнения среди делителей числа −8, являющимся свободным членом. Заметим, что 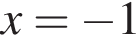 подходит, поэтому у многочлена есть множитель
подходит, поэтому у многочлена есть множитель ![]() Разложим многочлен на множители:
Разложим многочлен на множители:
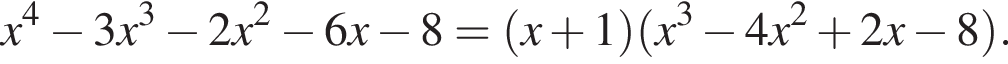
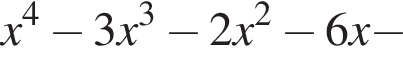
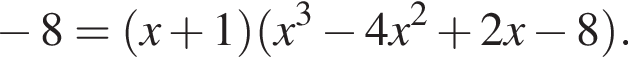
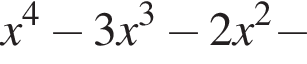

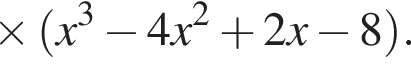
Второй множитель можно разложить на множители методом группировки:
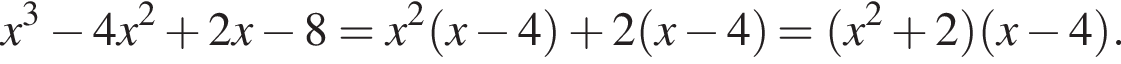
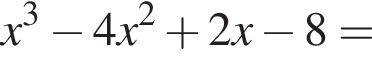
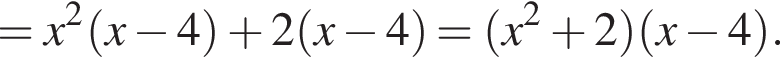
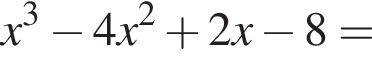
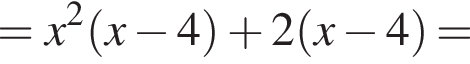
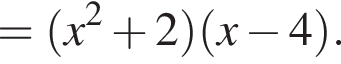
Значит, исходное уравнение можно записать в виде:
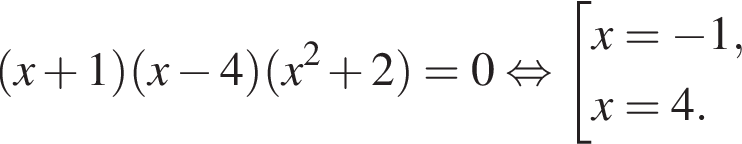
Ответ: 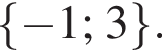
Ответ: 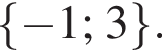
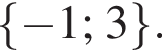
1205
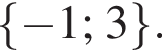
Классификатор алгебры: 3.7. Уравнения высших степеней
Методы алгебры: Группировка, разложение на множители