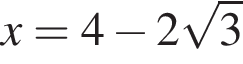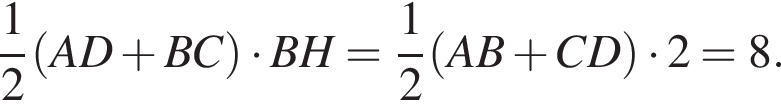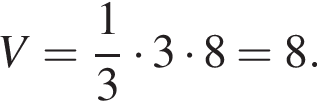Основанием пирамиды MABCD является трапеция ABCD с прямым углом A и основаниями BC = 3 см и AD = 6 см. Все боковые грани пирамиды образуют с основанием острый угол, синус которого равен 0,6. Найдите объем пирамиды.
Решение. Пусть точка O — проекция вершины M на плоскость ABCD. Перпендикуляры из точек O и M на каждое из ребер основания пирамиды падают в одну точку по теореме о трех перпендикулярах. Рассмотрим треугольник MOT, где T — любая из этих точек, тогда угол между боковой гранью пирамиды и плоскостью основания это угол MTO. Следовательно, все эти прямоугольные треугольники равны по общему катету MO и острому углу, поэтому вторые их катеты тоже равны. Итак, точка O равноудалена от всех сторон трапеции и поэтому является центром вписанной в неё окружности.
Проведем перпендикуляр CH к основанию AD трапеции. Тогда BCHA — прямоугольник,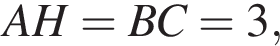 
и 
Обозначим 
тогда, по теореме Пифагора для треугольника CHD получаем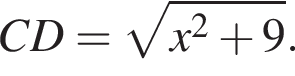 
Поскольку ABCD — описанный четырехугольник, суммы его противоположных сторон равны. Значит,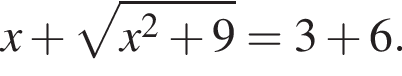 
Решим это уравнение:
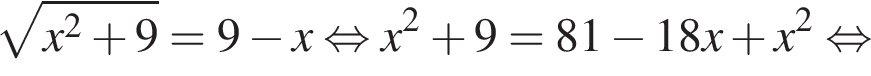
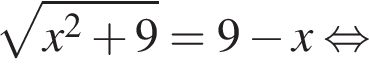
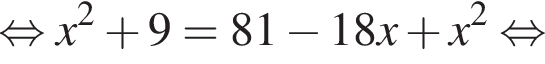
Поскольку расстояния от O до оснований трапеции равны, они равны половине высоты трапеции, то есть 2.
В треугольнике MOT теперь находим
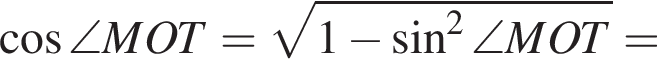
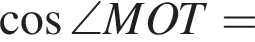
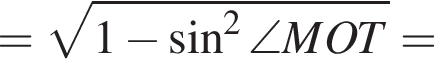
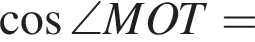
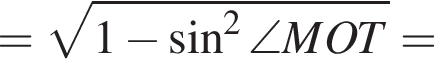
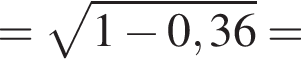
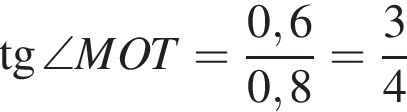и 
Это высота пирамиды. Площадь основания пирамиды равна
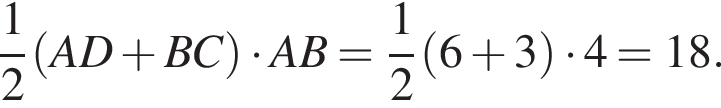
Окончательно, объем пирамиды равен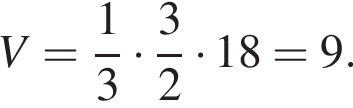 
Ответ: 9.
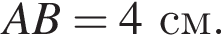
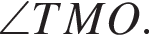Следовательно, все эти прямоугольные треугольники равны по общему катету TO и острому углу, поэтому вторые их катеты тоже равны. Итак, точка O равноудалена от всех сторон трапеции и поэтому является ее центром вписанной окружности. 
то
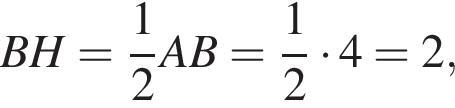
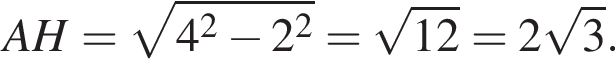
тогда
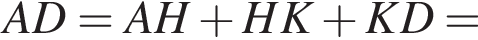
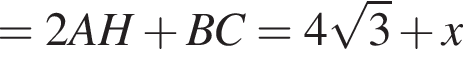
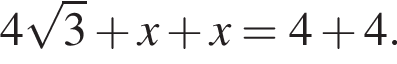Решим это уравнение. Получим: 
