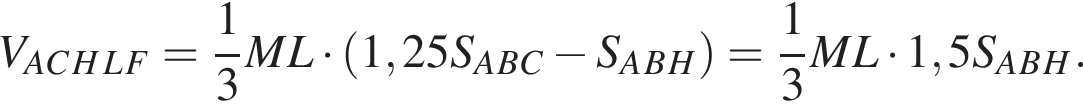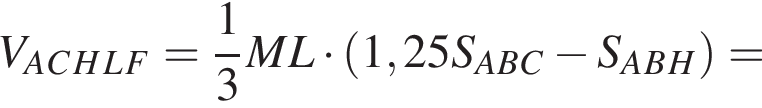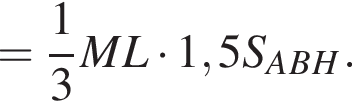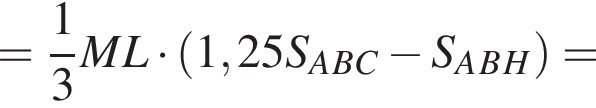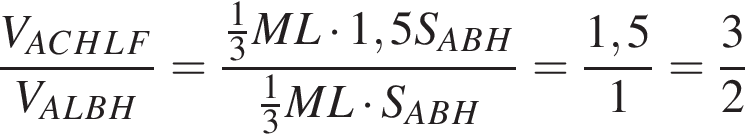Укажите номера уравнений, не имеющих корней:
а) 
б) 
в)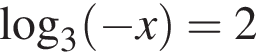 
г) 
Выберите верное утверждение:
а) у пятиугольной призмы десять ребер
б) призма является правильной, если ее боковые грани — прямоугольники
в) диагональным сечением прямой восьмиугольной призмы является треугольник
г) основаниями правильной призмы являются правильные многоугольники
Найдите наименьший положительный период функции 
Найдите наименьшее целое решение неравенства 
Решите уравнение 
Центральный угол в развертке боковой поверхности конуса равен 240°. Высота конуса равна 
см. Найдите его объем.
Найдите сумму наибольшего и наименьшего целых решений неравенства 
Найдите промежутки возрастания и убывания, а также точки минимума и максимума функции 
Найдите значение выражения 
В пирамиде FABC через медиану AH основания ABC и точке L бокового ребра BF (BL : LF = 4 : 1) проведена плоскость. Найдите отношение объема многогранника ACHLF к объему пирамиды ABLH.
является 
то наименьшим положительным периодом функции 
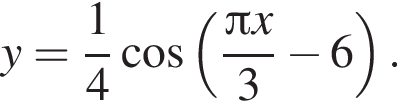
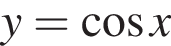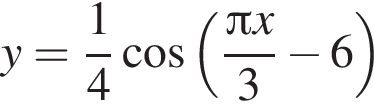является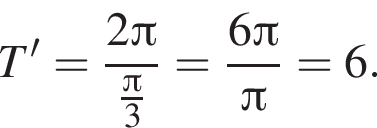
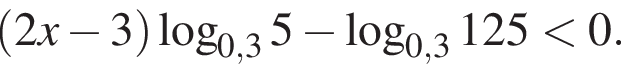
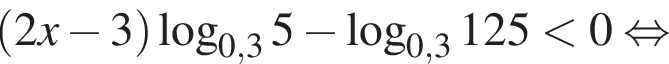
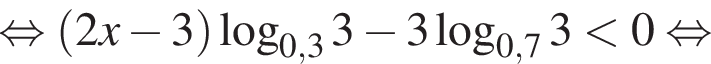
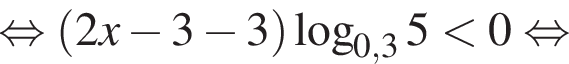
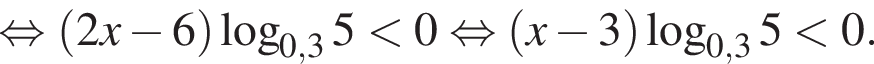
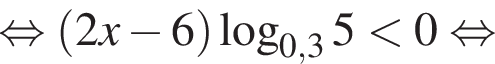
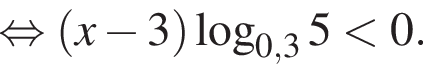
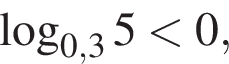так как 
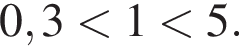Тогда разделим на это число и поменяем знак неравенства:
тогда радиус сектора также равен 
Находим длину дуги сектора 
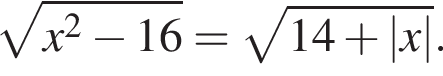
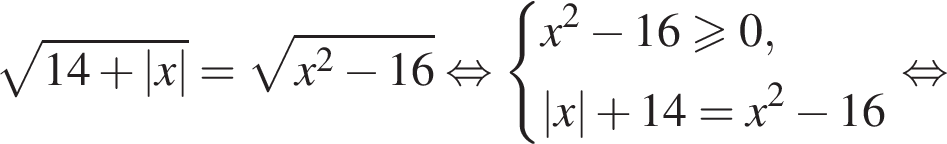
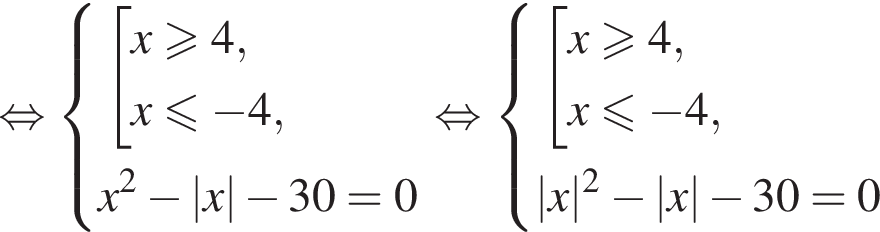
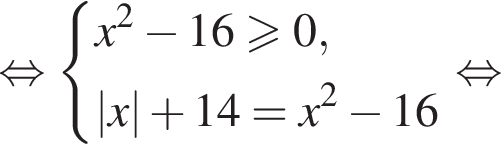
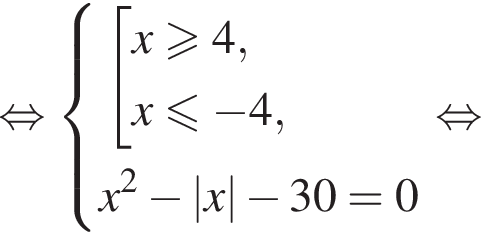
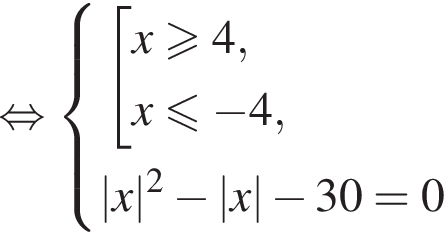
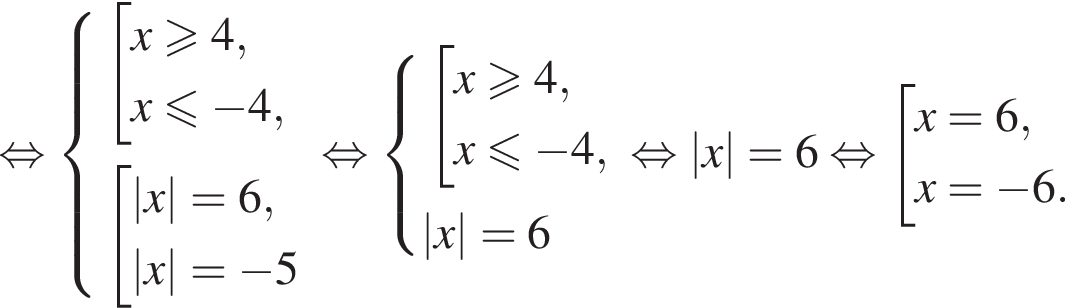
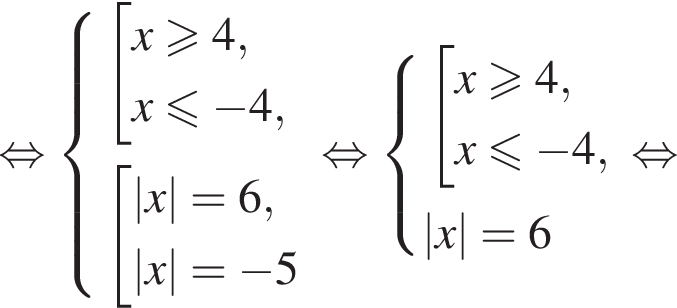
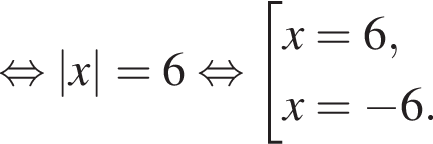
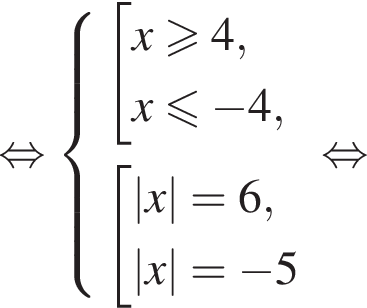
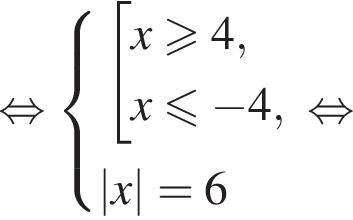
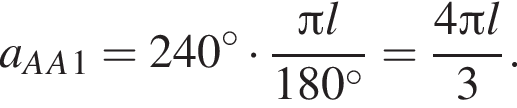Так как 
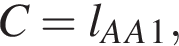то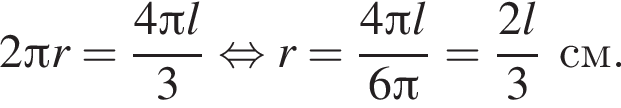 
В прямоугольном треугольнике POA по теореме Пифагора: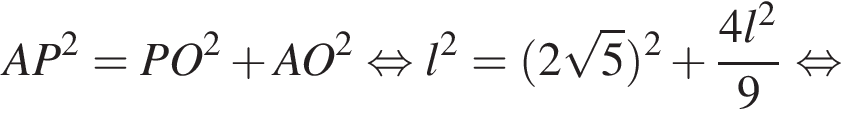
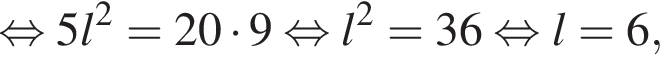
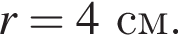
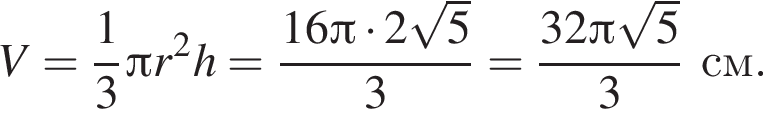
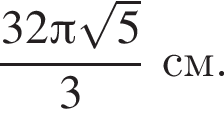
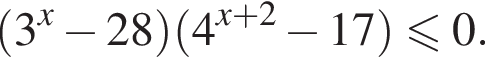
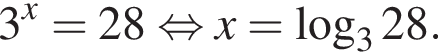
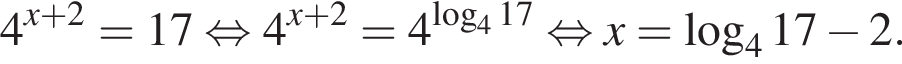
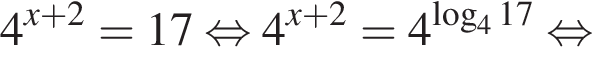
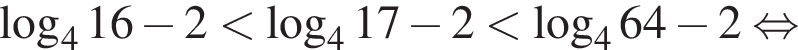
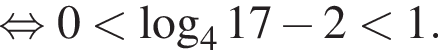
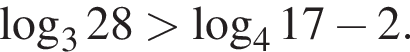Учитывая все отношения между числами, методом интервалов получаем, что 
Наименьшим и наибольшим решением неравенства являются числа 1 и 3 соответственно (см. изображение).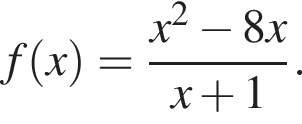
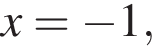значит, 
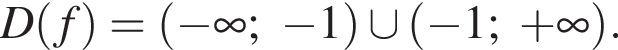Теперь найдем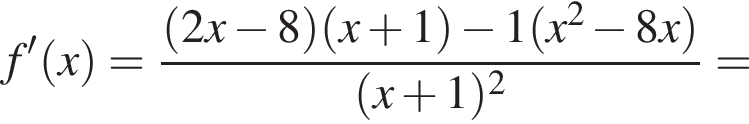 
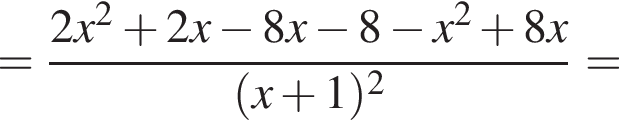
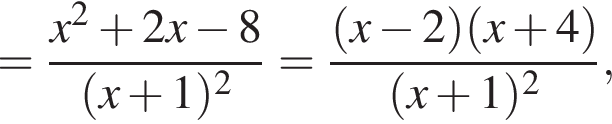
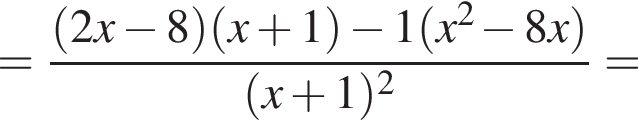
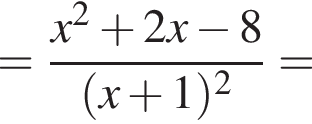
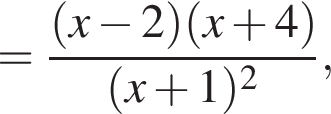
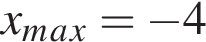и 
и на 
а убывает на промежутках 
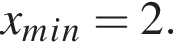
и на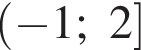 
(см. изображение).
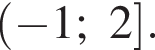Максимум и минимум функции соответственно равны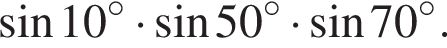 
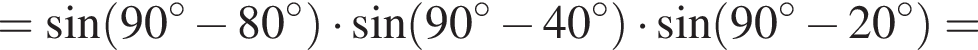
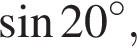затем применим формулы синуса двойного аргумента: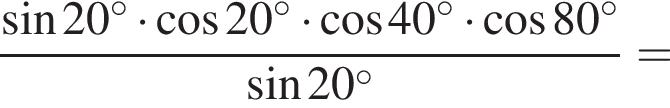
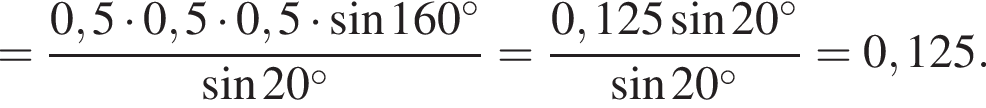
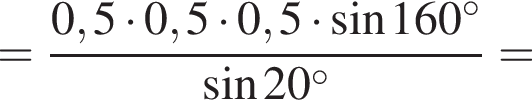
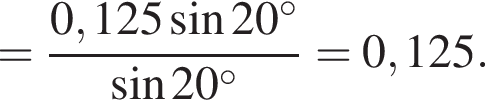
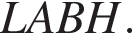В треугольниках FBN и LBM угол 
— общий, а углы 
и 
— прямые, значит, эти треугольники подобны по двум углам, откуда: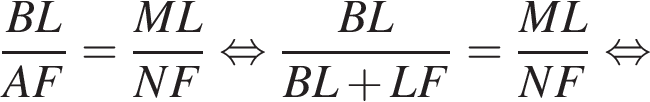
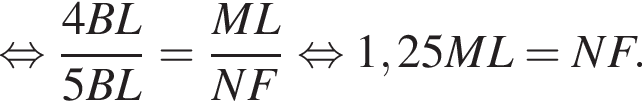
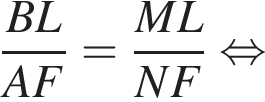
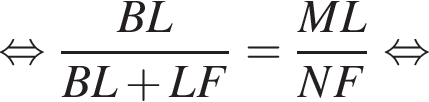
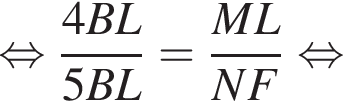
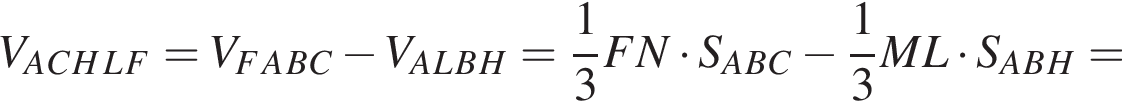
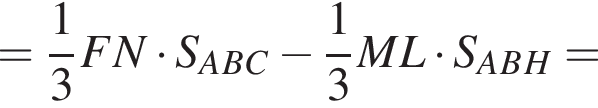
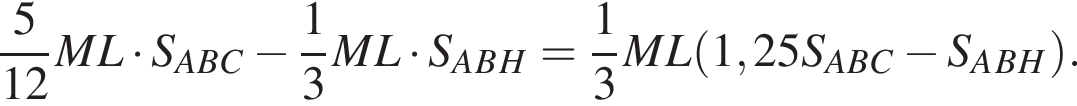
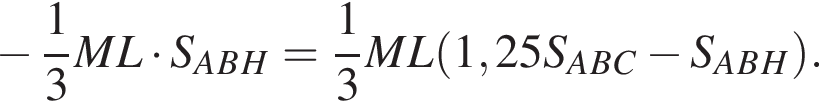
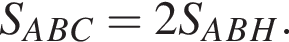Тогда:
