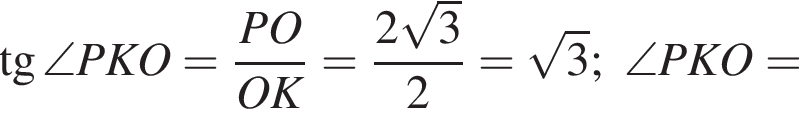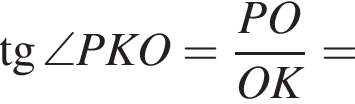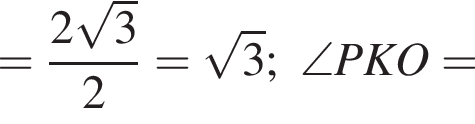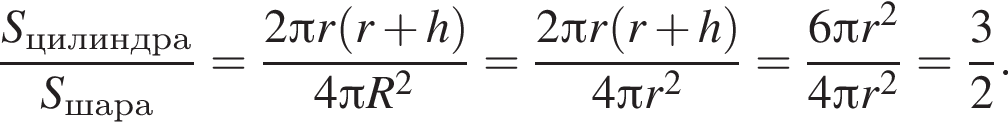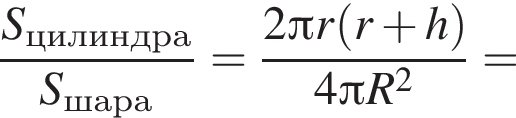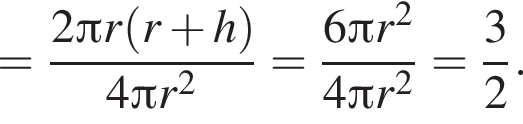В треугольной пирамиде все плоские углы при вершине прямые. Боковые ребра пирамиды равны 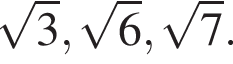 Найдите объем описанного около пирамиды шара.
Найдите объем описанного около пирамиды шара.
В кубе ABCDA1B1C1D1 диагональ AC1 равна ![]() Точки M и H — середины ребер B1C1, D1C1 соответственно, а точка P принадлежит ребру DD1, причем D1P : DD 1 = 1 : 3. Найдите периметр сечения куба плоскостью MHP.
Точки M и H — середины ребер B1C1, D1C1 соответственно, а точка P принадлежит ребру DD1, причем D1P : DD 1 = 1 : 3. Найдите периметр сечения куба плоскостью MHP.
Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны 2, 2 и 4. Найдите радиус описанной около этой пирамиды сферы.
В конус вписана прямая шестиугольная призма так, что нижнее ее основание лежит на основании конуса, а вершины верхнего основания лежат на боковой поверхности конуса. Все ребра призмы равны. Найдите отношение полных поверхностей конуса и призмы, если осевое сечение конуса является правильным треугольником.
Дан конус, радиус основания которого равен высоте. Найдите двугранный угол при боковом ребре правильной четырехугольной пирамиды, вписанной в конус.
Куб, шар и конус, осевым сечением которого является правильный треугольник, имеют равные площади полных поверхностей. Найдите, какая из данных фигур имеет наименьший объем.
Апофема правильной треугольной пирамиды ![]() см. Центр вписанного в пирамиду шара отстоит от вершины пирамиды на расстоянии, вдвое больше радиуса шара. Найдите площадь боковой поверхности пирамиды.
см. Центр вписанного в пирамиду шара отстоит от вершины пирамиды на расстоянии, вдвое больше радиуса шара. Найдите площадь боковой поверхности пирамиды.
Точки M и K являются соответственно серединами ребер B1C1 и A1B1 куба ABCDA1B1C1D1. Точка H принадлежит ребру AA1, причем AH : AA1 = 2 : 3. Найдите периметр сечения куба плоскостью MHK, если диагональ BD1 равна ![]()
В правильную четырехугольную пирамиду вписан куб так, что четыре вершины куба лежат на основании пирамиды, а противоположные им вершины принадлежат боковым ребрам пирамиды. Найдите ребро куба, если высота пирамиды равна ![]() см, а сторона основания пирамиды равна
см, а сторона основания пирамиды равна ![]() см.
см.
В правильную четырехугольную пирамиду вписан конус, и около нее описан конус. Найдите разность объемов описанного и вписанного конусов, если высота пирамиды равна 8, а длина окружности основания вписанного конуса равна ![]()
В треугольной пирамиде все плоские углы при вершине прямые. Боковые ребра пирамиды равны 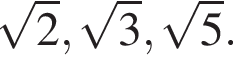 Найдите площадь поверхности описанной около пирамиды сферы.
Найдите площадь поверхности описанной около пирамиды сферы.
Плоскость пересекает основания цилиндра по хордам, равным 6 и 8 см, расстояние между которыми равно 9 см. Найдите площадь поверхности цилиндра, если радиус основания равен 5 см и плоскость пересекает ось цилиндра во внутренней его точке.
Осевое сечение конуса имеет прямой угол при вершине. Площадь боковой поверхности конуса — ![]() см2. Найдите площадь сферы, вписанной в конус.
см2. Найдите площадь сферы, вписанной в конус.
Каждое ребро треугольной пирамиды равна a. Найдите радиус сферы, описанной около пирамиды.
Конус описан около пирамиды PABCD, основанием которой является трапеция ABCD. Известно, что AB=BC=CD=3 см и один из углов трапеции равен 60°. Объем конуса равен ![]() см3. Найдите угол наклона боковых ребер пирамиды к плоскости основания.
см3. Найдите угол наклона боковых ребер пирамиды к плоскости основания.
Вершины квадрата принадлежат окружностям верхнего и нижнего оснований цилиндра. Найдите площадь поверхности цилиндра, если радиус основания цилиндра равен 7 см, сторона квадрата — 10 см и плоскость квадрата пересекает ось цилиндра.
Двугранный угол при боковом ребре правильной четырехугольной пирамиды равен 120°. Высота пирамиды равна 5. Найдите объем конуса, вписанного в эту пирамиду.
Боковое ребро правильной треугольной пирамиды равно 1 см, а радиус описанной около пирамиды сферы равен 1 см. Найдите объем пирамиды.
В треугольную пирамиду, все ребра которой равны между собой, вписан шар, радиус которого равен ![]() см. Найдите объем пирамиды.
см. Найдите объем пирамиды.
Тело состоит из двух конусов, имеющих общее основание и расположенных по разные стороны от плоскости основания. Найдите площадь сферы, вписанной в тело, если радиус основания конусов равен 2, а образующие равны ![]() и
и ![]()
Образующая конуса наклонена к плоскости основания под углом 30°. Площадь осевого сечения конуса равна 75 см2. Найдите площадь поверхности сферы, описанной около этого конуса.
Решите уравнение 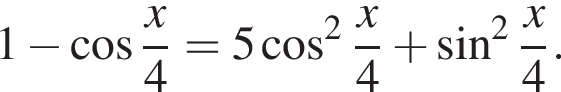
В правильную треугольную пирамиду вписан конус, и около нее описан конус. Найдите разность объемов описанного и вписанного конусов, если высота пирамиды равна 4, а длина окружности основания описанного конуса равна ![]()
Точка пересечения диагоналей основания правильной четырехугольной пирамиды делит отрезок, соединяющий вершину пирамиды с центром описанной около пирамиды сферы, в отношении 5 : 3, считая от вершины. Найдите угол наклона бокового ребра пирамиды к плоскости ее основания.
Найдите, в каком отношении делит высоту конуса плоскость, параллельная основанию, если полученные меньший конус и усеченный конус имеют равные площади полных поверхностей, а образующая и радиус основания исходного конуса равны 16 и 10 соответственно.
Боковые ребра треугольной пирамиды имеют одинаковую длину и равны 15 см. Из трех плоских углов, образованных этими ребрами при вершине пирамиды, два равны 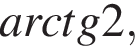 а третий — 90°. Найдите объем пирамиды.
а третий — 90°. Найдите объем пирамиды.
Около цилиндра, осевое сечение которого — квадрат, описана треугольная призма, объем которой равен 672 см3, а площадь полной поверхности — 504 см2. Вычислите площадь полной поверхности цилиндра.
Основание прямой призмы — равнобедренный треугольник с основанием a и углом при основании ![]() Диагональ боковой грани, содержащей боковую сторону треугольника, наклонена к плоскости основания под углом
Диагональ боковой грани, содержащей боковую сторону треугольника, наклонена к плоскости основания под углом ![]() Найдите площадь боковой поверхности цилиндра, вписанного в призму.
Найдите площадь боковой поверхности цилиндра, вписанного в призму.
Основанием конуса служит круг, описанный около основания правильной треугольной призмы. Вершина конуса лежит на другом основании призмы. Найдите объем призмы, если объем конуса равен ![]() см2.
см2.
Образующая конуса равна диаметру его основания, площадь боковой поверхности конуса равна 72![]() см2. Куб вписан в конус так, что одна из граней куба принадлежит основанию конуса, а вершины противолежащей грани принадлежат боковой поверхности конуса. Найдите ребро куба, вписанного в конус.
см2. Куб вписан в конус так, что одна из граней куба принадлежит основанию конуса, а вершины противолежащей грани принадлежат боковой поверхности конуса. Найдите ребро куба, вписанного в конус.
Двугранный угол при боковом ребре правильной треугольной пирамиды равен 120°. Высота пирамиды равна 3. Найдите объем конуса, описанного около этой пирамиды.
Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны 8, 5 и 6 см. Через точку, взятую на высоте пирамиды и делящую высоту в отношении 1 : 3, считая от вершины, проведена плоскость, параллельная основанию пирамиды. Найдите объем большей из образовавшихся частей пирамиды.
Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны 6, 4 и 4. Найдите радиус описанной около этой пирамиды сферы.
Тело состоит из двух конусов, имеющих общее основание и расположенных по разные стороны от плоскости основания. Найдите площадь поверхности шара, вписанного в тело, если радиус основания конусов равен 1, а высоты — 1 и 2.
Угол между высотой правильной треугольной пирамиды и боковой гранью равен 30°. Найдите площадь боковой поверхности пирамиды, если радиус вписанного в пирамиду шара равен 1 см.
Шар вписан в цилиндр. Найдите отношение объема шара к объему цилиндра.
В пирамиде FABC через медиану BK основания ABC и точке L бокового ребра AF (AL : LF = 1 : 3) проведена плоскость. Найдите отношение объема многогранника BCKLF к объему пирамиды ABLK.
Боковые ребра треугольной пирамиды имеют одинаковую длину и равны 10 см. Из трех плоских углов, образованных этими ребрами при вершине пирамиды, два равны  а третий — 60°. Найдите объем пирамиды.
а третий — 60°. Найдите объем пирамиды.
Образующая конуса наклонена к основанию под углом 60°, площадь полной поверхности конуса равна ![]() см2. Куб вписан в конус так, что одна из граней куба принадлежит основанию конуса, а вершины противолежащей грани принадлежит боковой поверхности конуса. Найдите ребро куба, вписанного в конус.
см2. Куб вписан в конус так, что одна из граней куба принадлежит основанию конуса, а вершины противолежащей грани принадлежит боковой поверхности конуса. Найдите ребро куба, вписанного в конус.
Основанием конуса служит круг, вписанный в основание правильной треугольной призмы. Вершина конуса лежит на другом основании призмы. Найдите объем призмы, если объем конуса равен ![]() см2.
см2.
ABCDA1B1C1D1 — прямоугольный параллелепипед, причем ABCD — квадрат со стороной ![]() а ребро AA1 равно
а ребро AA1 равно ![]() Найдите периметр сечения, проведенного через точки C, K и M, где K и M — середины ребер AD и BB1 соответственно.
Найдите периметр сечения, проведенного через точки C, K и M, где K и M — середины ребер AD и BB1 соответственно.
Центр сферы, описанной около правильной четырехугольной пирамиды, делит ее высоту в отношении 5 : 3, считая от вершины. Найдите угол наклона бокового ребра пирамиды к плоскости ее основания.
Найдите, в каком отношении делит высоту конуса плоскость, параллельная основанию, если площадь полной поверхности отсеченного конуса равна половине площади поверхности всего конуса, а радиус основания и образующая исходного конуса равны 2 и 6 соответственно.
В правильную четырехугольную пирамиду вписан цилиндр, осевым сечением которого является квадрат, так, что одно основание цилиндра лежит на основании пирамиды, а другое основание цилиндра касается боковых граней пирамиды. Найдите объем цилиндра, если высота пирамиды равна ![]() см, а сторона основания пирамиды равна
см, а сторона основания пирамиды равна ![]() см.
см.
Боковые грани правильной четырёхугольной призмы — квадраты. Площадь боковой поверхности призмы равна 100. Найдите объем многогранника, вершинами которого являются центры всех граней призмы.
Каждое ребро треугольной пирамиды равно a. Найдите радиус вписанной в нее сферы.
Высота конуса равна 3 см, угол между высотой и образующей равен 30°. В этот конус вписан другой конус так, что его вершина совпадает с центром основания первого конуса, а соответствующие образующие взаимно перпендикулярны. Найдите объем вписанного конуса.
Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны 4, 5 и 6 см. Через точку, взятую на высоте пирамиды и делящую высоту в отношении 1 : 2, считая от вершины, проведена плоскость, параллельная основанию пирамиды. Найдите объем большей из образовавшихся частей пирамиды.
Центр шара радиусом R совпадает с центром основания конуса. Образующие конуса касаются данного шара на расстоянии 0,5R от основания конуса. Найдите отношение площадей поверхностей шара и конуса.
Сторона основания правильной треугольной пирамиды равна ![]() см, а радиус описанного около пирамиды шара равен
см, а радиус описанного около пирамиды шара равен ![]() см. Найдите объем пирамиды.
см. Найдите объем пирамиды.
В правильную четырехугольную пирамиду вписан куб так, что четыре вершины куба лежат на основании пирамиды, а противоположные им вершины принадлежат боковым ребрам пирамиды. Найдите ребро куба, если высота пирамиды равна ![]() см, а сторона основания пирамиды равна
см, а сторона основания пирамиды равна ![]() см.
см.
Дан конус, радиус основания которого относится к высоте как 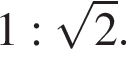 Найдите угол между плоскостями боковых граней правильной треугольной пирамиды, вписанной в конус.
Найдите угол между плоскостями боковых граней правильной треугольной пирамиды, вписанной в конус.
Около цилиндра, осевое сечение которого — квадрат, описана треугольная призма, периметр основания которой равен 14 см, а площадь полной поверхности — 56 см2. Вычислите площадь боковой поверхности цилиндра.
Образующая конуса равна 4 см, площадь осевого сечения равна 4 см2. Найдите, во сколько раз площадь основания конуса меньше площади его боковой поверхности, если угол при вершине осевого сечения тупой.
Основание прямой призмы — равнобедренный треугольник с боковой стороной b и углом при основании ![]() Диагональ боковой грани, содержащей основание треугольника, образует с боковым ребром угол
Диагональ боковой грани, содержащей основание треугольника, образует с боковым ребром угол ![]() Найдите площадь боковой поверхности цилиндра, вписанного в призму.
Найдите площадь боковой поверхности цилиндра, вписанного в призму.
В правильной треугольной пирамиде угол между боковой гранью и плоскостью основания равен 45![]() В пирамиду вписан цилиндр, нижнее основание которого лежит на основании пирамиды, а окружность его верхнего основания касается боковых граней пирамиды. Найдите отношение объемов пирамиды и цилиндра, если осевое сечение цилиндра является квадратом.
В пирамиду вписан цилиндр, нижнее основание которого лежит на основании пирамиды, а окружность его верхнего основания касается боковых граней пирамиды. Найдите отношение объемов пирамиды и цилиндра, если осевое сечение цилиндра является квадратом.
В шар радиусом R помещен конус так, что его вершина совпадает с центром шара, а основание касается поверхности шара. Отношение боковой поверхности конуса к поверхности шара равно 1 : 8. Найдите расстояние от центра шара до основания конуса.
В пирамиде FABC через медиану AH основания ABC и точке L бокового ребра BF (BL : LF = 4 : 1) проведена плоскость. Найдите отношение объема многогранника ACHLF к объему пирамиды ABLH.
Образующая конуса равна 2 см, площадь осевого сечения равна 2 см2. Найдите, во сколько раз площадь полной поверхности конуса больше площади основания.
В правильную четырехугольную пирамиду вписан конус. Найдите объем конуса, если объем пирамиды равен ![]() см3.
см3.
Осевое сечение конуса имеет угол при вершине, равный 120°. Объем конуса — ![]() см3. Найдите площадь сферы, описанной вокруг конуса.
см3. Найдите площадь сферы, описанной вокруг конуса.
Около правильной четырехугольной пирамиды описан конус. Найдите объем конуса, если объем пирамиды равен ![]() см3.
см3.
Найдите объем шара, вписанного в треугольную пирамиду, все ребра которой равны ![]() см.
см.
В правильную четырехугольную пирамиду вписан цилиндр, осевым сечением которого является квадрат, так, что одно основание цилиндра лежит на основании пирамиды, а другое основание цилиндра касается боковых граней пирамиды. Найдите объем цилиндра, если высота пирамиды равна ![]() см, а сторона основания пирамиды равна
см, а сторона основания пирамиды равна ![]() см.
см.
Боковые грани правильной треугольной призмы — квадраты. Площадь боковой поверхности призмы равна 108. Найдите объем многогранника, вершинами которого являются центры всех граней призмы.
Основание прямоугольного параллелепипеда ABCDA1B1C1D1 — квадрат ABCD со стороной ![]() длина ребра AA1 =
длина ребра AA1 = ![]() Найдите периметр сечения, проведенного через точки C, P и M, где P — середина AD, M — середина BB1.
Найдите периметр сечения, проведенного через точки C, P и M, где P — середина AD, M — середина BB1.
Конус вписан в пирамиду, основанием которой является равнобедренная трапеция с основаниями 2 и 8 см. Объем конуса равен ![]() см3. Найдите угол наклона боковых граней пирамиды к плоскости основания.
см3. Найдите угол наклона боковых граней пирамиды к плоскости основания.
Вокруг шара описан цилиндр. Найдите отношение площади поверхности цилиндра к площади поверхности шара.



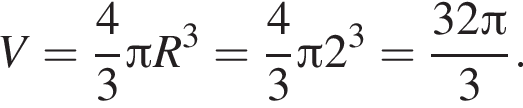
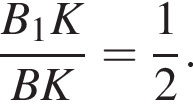 Так как диагональ куба равна
Так как диагональ куба равна 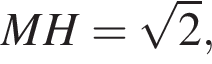 а отрезки KM и HP равны
а отрезки KM и HP равны 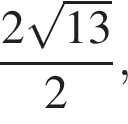 тогда периметр сечения равен:
тогда периметр сечения равен: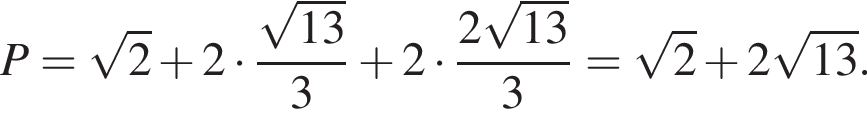
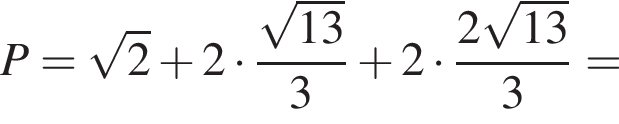
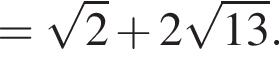
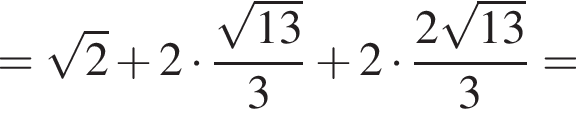
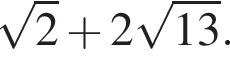




 ADC — основание пирамиды. По теореме Пифагора в треугольнике ADC гипотенуза AC равна
ADC — основание пирамиды. По теореме Пифагора в треугольнике ADC гипотенуза AC равна 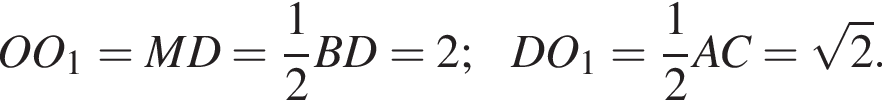
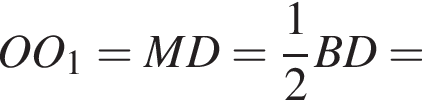
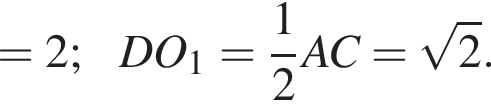
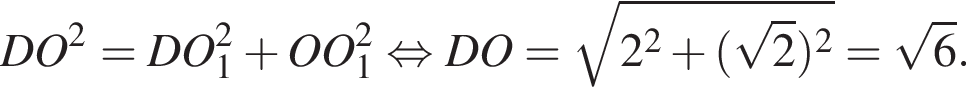
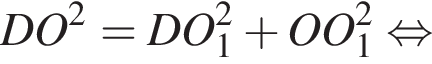
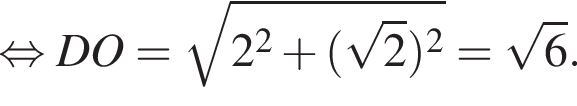
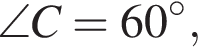 получаем, что:
получаем, что: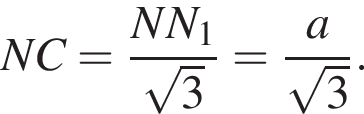
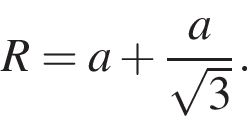 Образующая конуса равна:
Образующая конуса равна: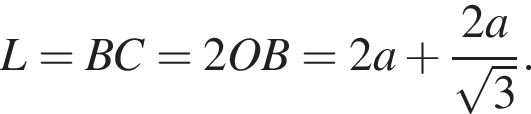

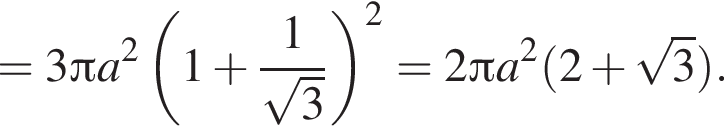
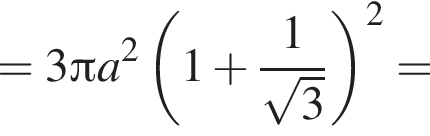
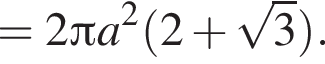
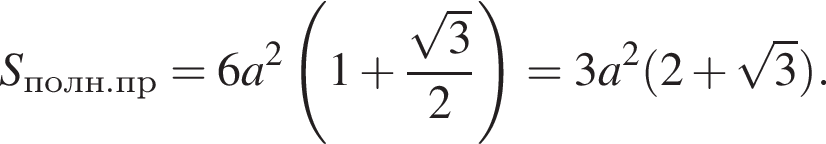
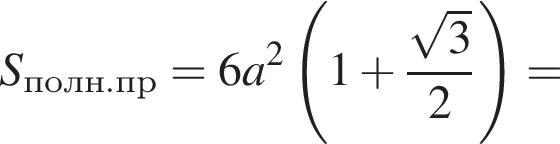
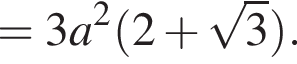
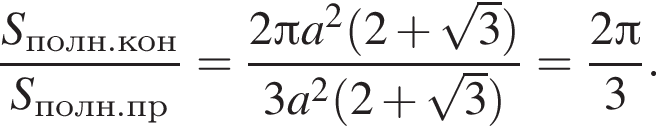
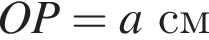 и
и  так как основание пирамиды — вписанный в окружность квадрат. В прямоугольном треугольнике
так как основание пирамиды — вписанный в окружность квадрат. В прямоугольном треугольнике 

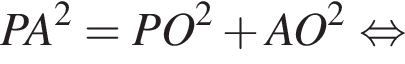
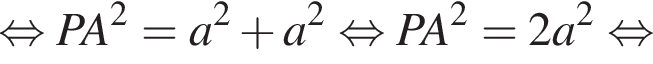
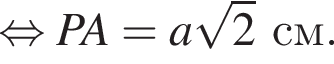
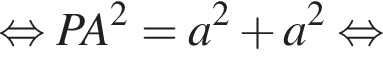


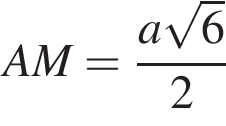 и
и  равен углу между боковыми гранями пирамиды. По теореме косинусов в треугольнике AMC:
равен углу между боковыми гранями пирамиды. По теореме косинусов в треугольнике AMC: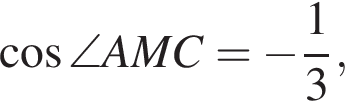 откуда
откуда 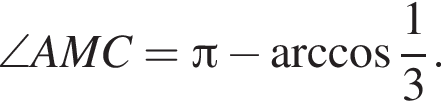
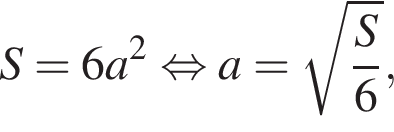
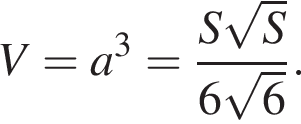
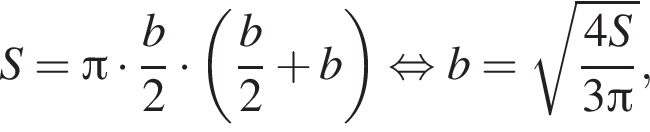
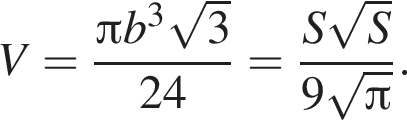
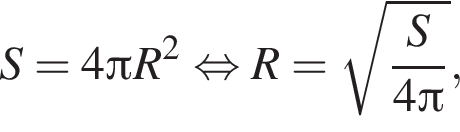
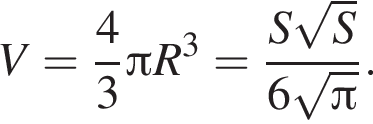

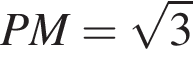 см и PO = 2HO.
см и PO = 2HO.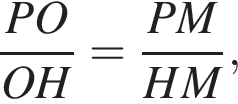 отсюда
отсюда 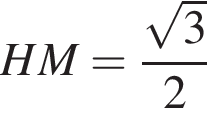 см.
см.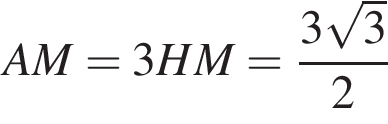 см и
см и 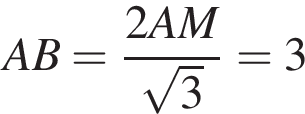 см.
см.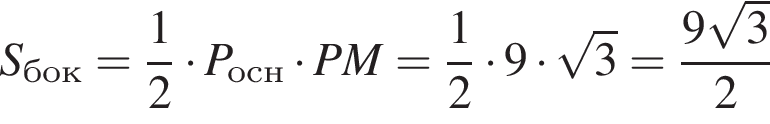 см2.
см2.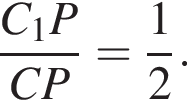 Так как диагональ куба равна
Так как диагональ куба равна 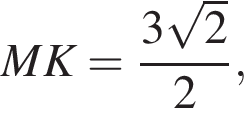 а отрезки KH и MP равны
а отрезки KH и MP равны 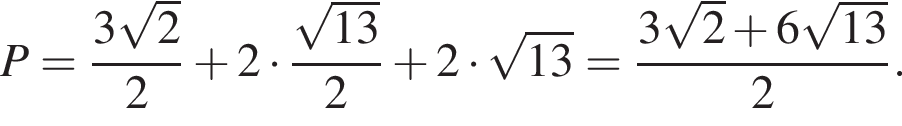
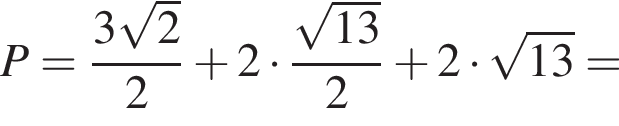
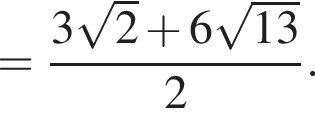
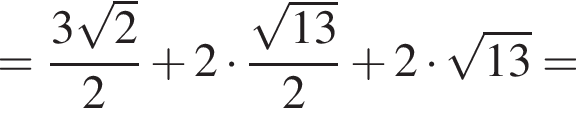
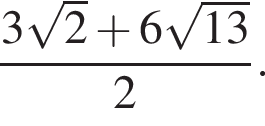
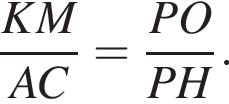
 аналогично
аналогично 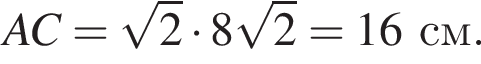 Из условия
Из условия 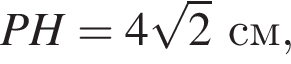 следовательно,
следовательно, 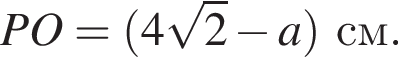 Подставим данные в отношения, полученные из подобия, и найдем a:
Подставим данные в отношения, полученные из подобия, и найдем a: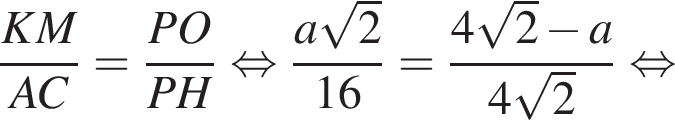
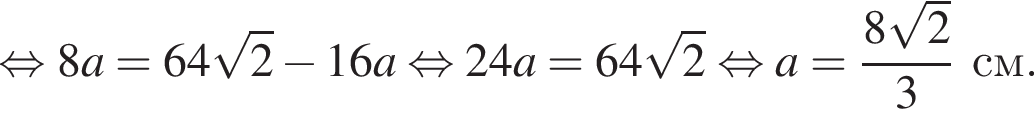
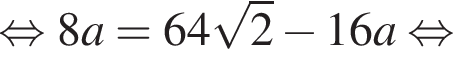
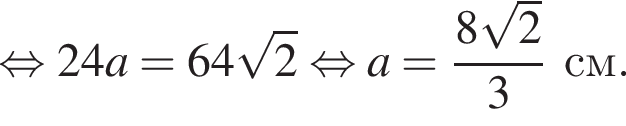
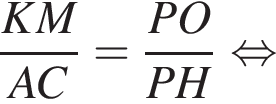
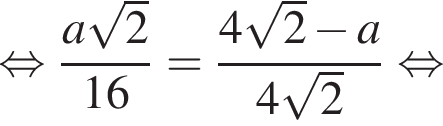
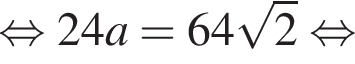
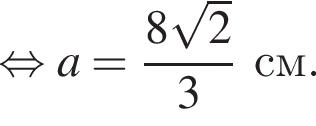
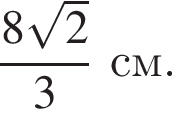
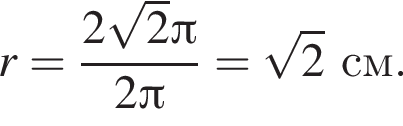
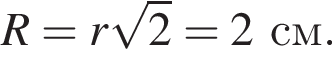
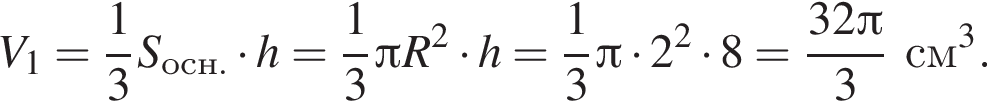
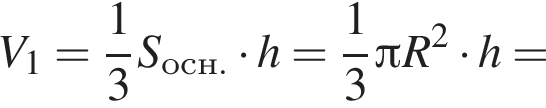
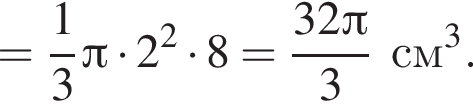
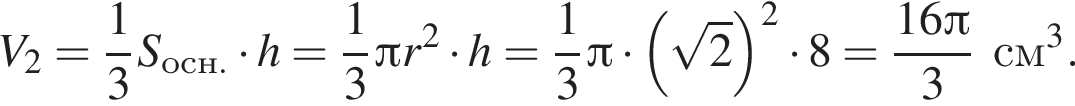
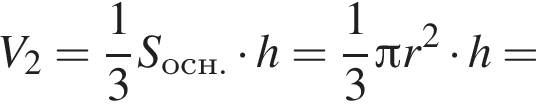
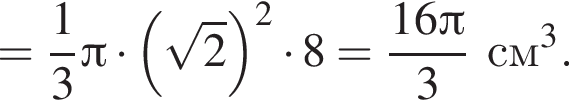
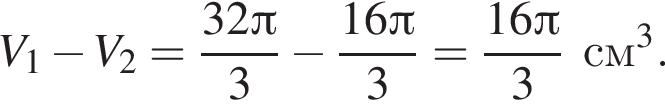
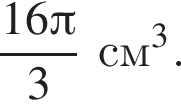
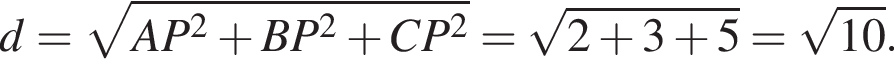
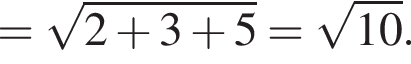
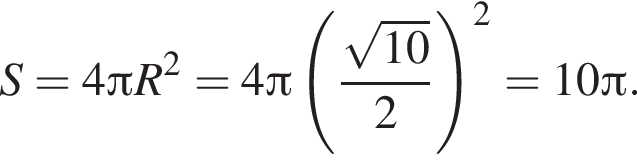
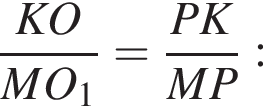
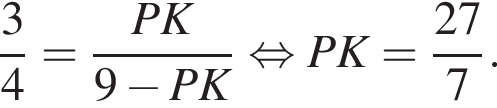
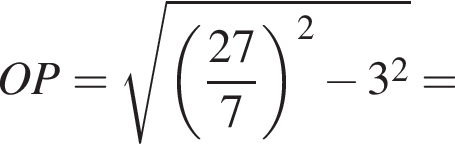
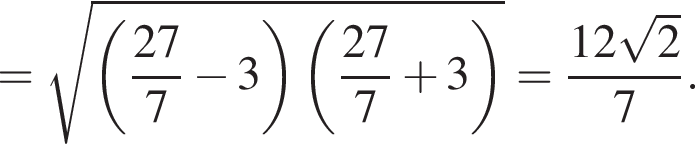
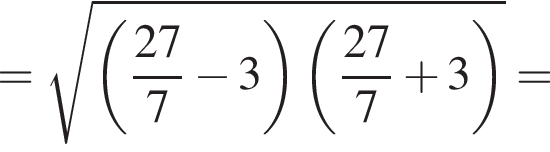
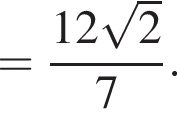
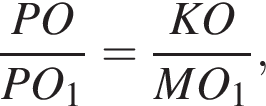 получаем, что
получаем, что 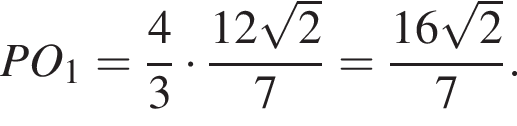
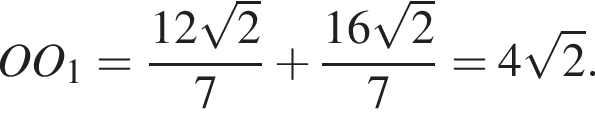

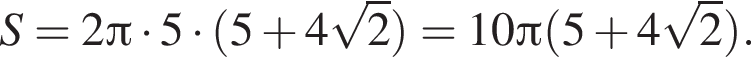
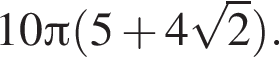
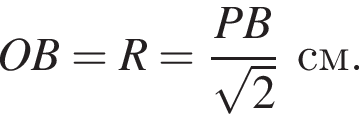 По формуле площади боковой поверхности
По формуле площади боковой поверхности 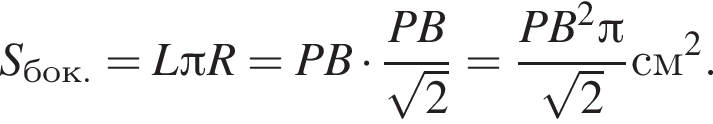
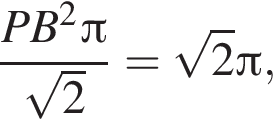 значит,
значит, 
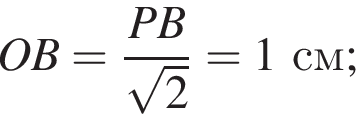 AB = 2OB = 2 см.
AB = 2OB = 2 см.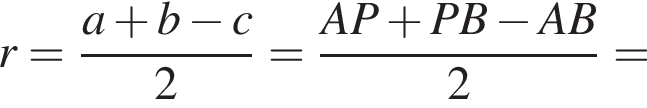
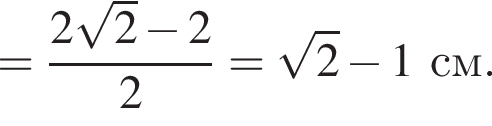
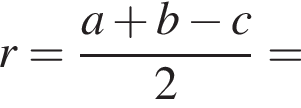
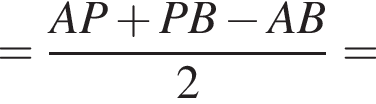
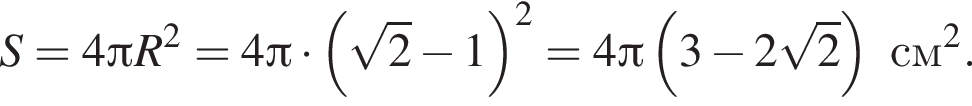
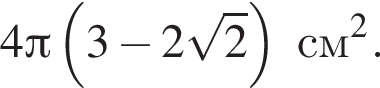
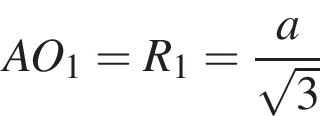 как радиус описанной около треугольника ABC окружности. Имеем:
как радиус описанной около треугольника ABC окружности. Имеем: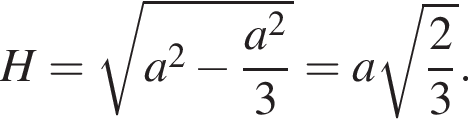
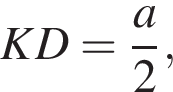 DO = AO = R — радиус описанной сферы. Из подобия треугольников OKD и AO1D имеем:
DO = AO = R — радиус описанной сферы. Из подобия треугольников OKD и AO1D имеем: 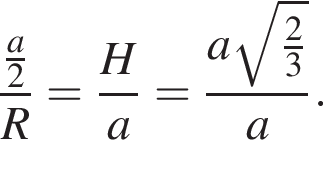 Откуда искомый радиус
Откуда искомый радиус 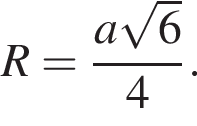
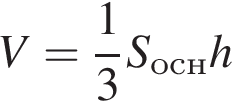 найдём высоту:
найдём высоту: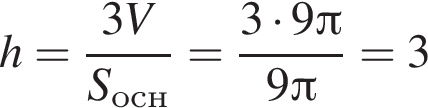 см.
см.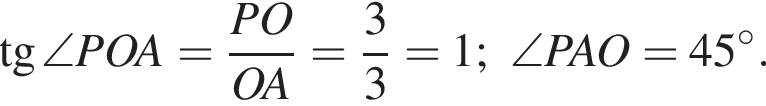
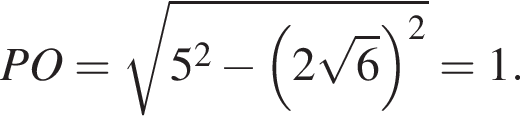
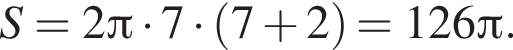
 Треугольник DKB — равнобедренный, DK = BK, тогда
Треугольник DKB — равнобедренный, DK = BK, тогда  Воспользуемся теоремой синусов:
Воспользуемся теоремой синусов: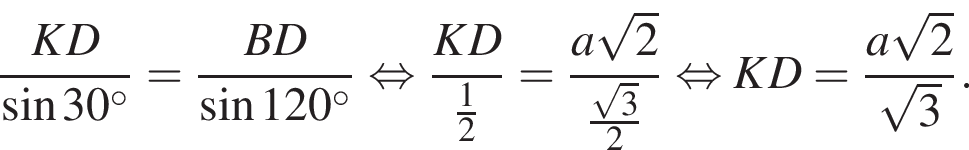
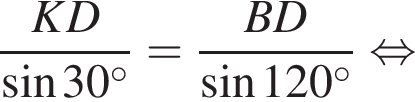
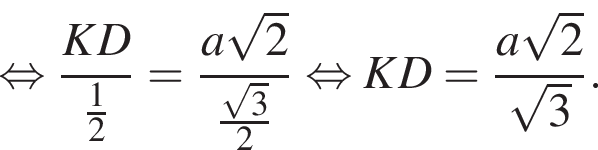
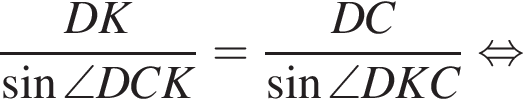
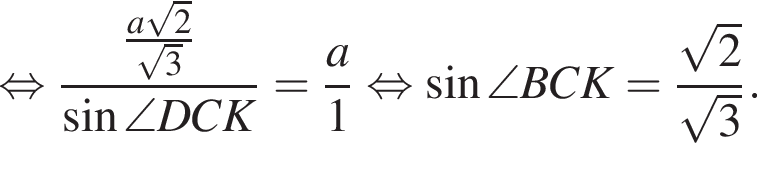
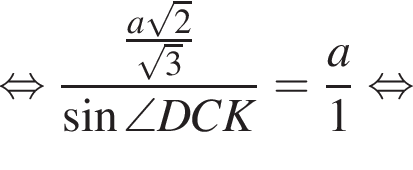
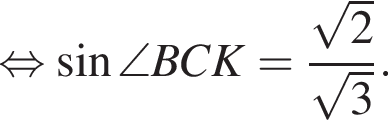
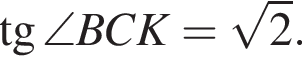
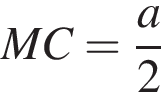 и
и 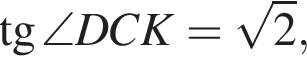 тогда
тогда 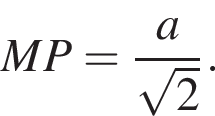 Так как ABC квадрат, то H — центр квадрата, откуда
Так как ABC квадрат, то H — центр квадрата, откуда 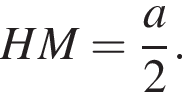
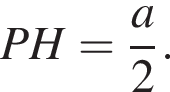 По условию высота пирамиды равна 5, тогда:
По условию высота пирамиды равна 5, тогда: 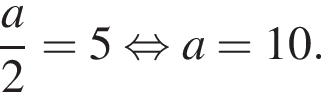
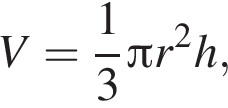 где r = 5, h = 5:
где r = 5, h = 5: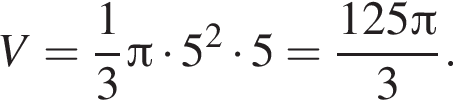
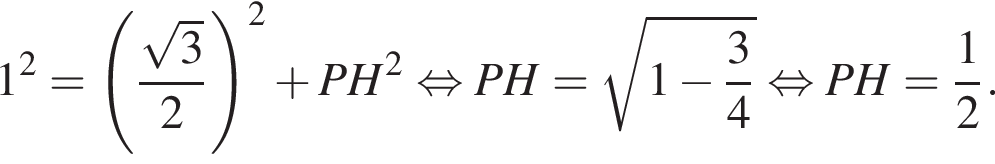
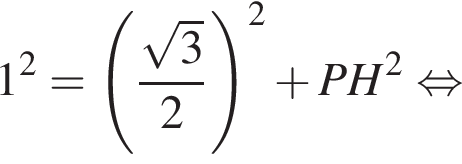
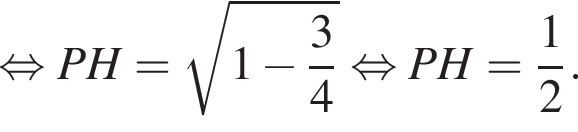
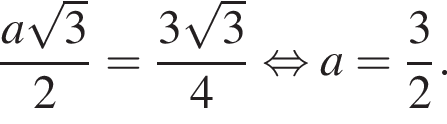
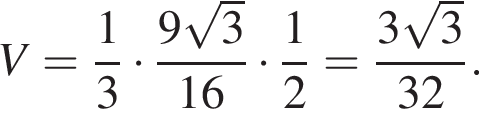
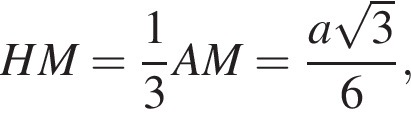 где a — ребро пирамиды. Апофема PM — высота треугольника PBC, значит,
где a — ребро пирамиды. Апофема PM — высота треугольника PBC, значит, 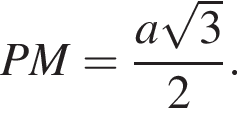 По теореме Пифагора в треугольнике PMH:
По теореме Пифагора в треугольнике PMH: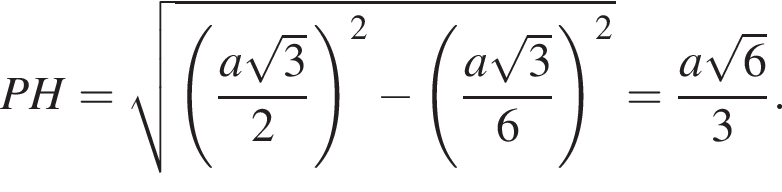
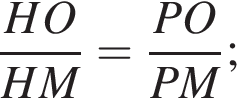
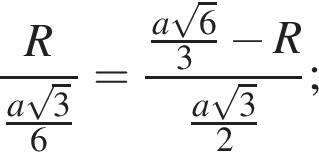
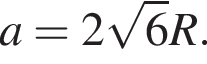


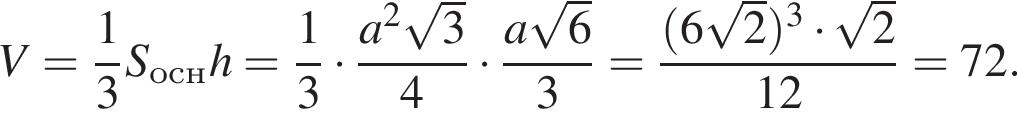
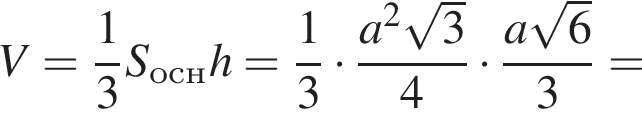
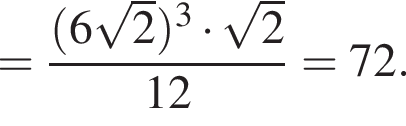
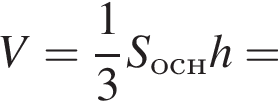
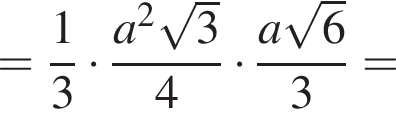

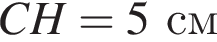 и
и 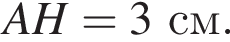
 откуда
откуда 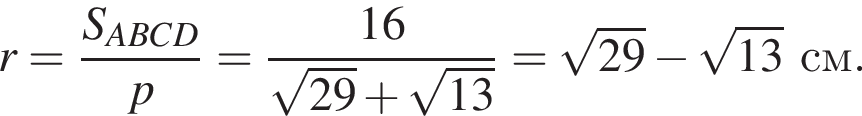
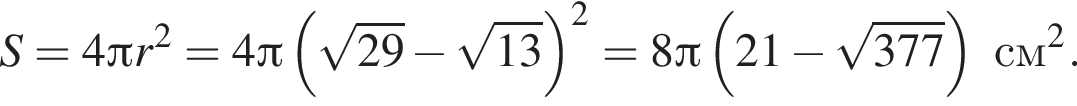
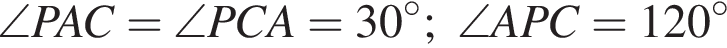 ). Найдем полощадь треугольника APK:
). Найдем полощадь треугольника APK: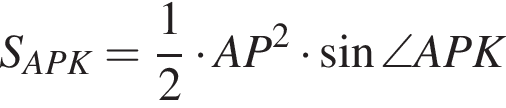 (см.рис.).
(см.рис.).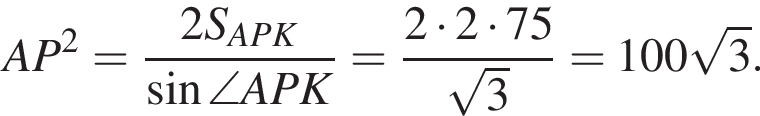
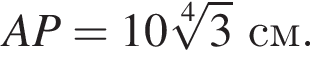 По теореме синусов из треугольника APK:
По теореме синусов из треугольника APK: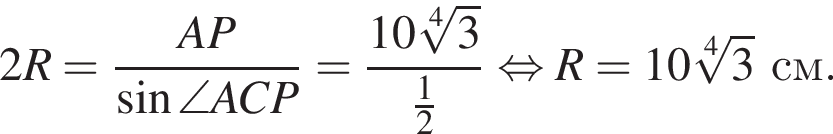
 :
: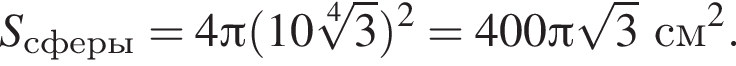

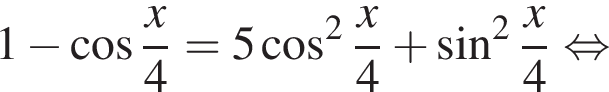
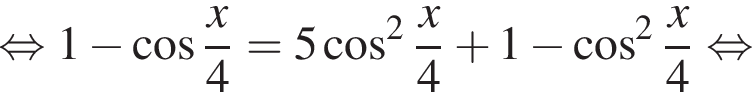
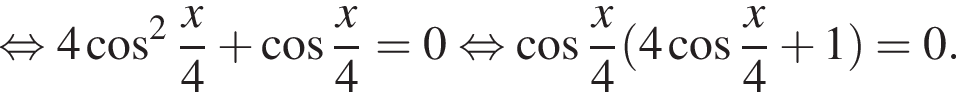
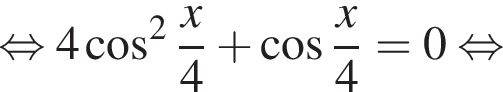
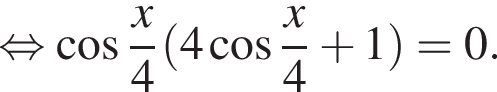
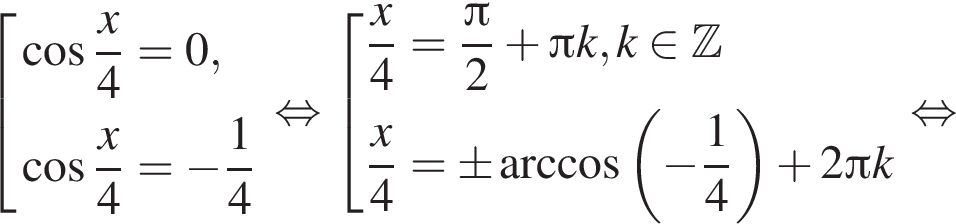
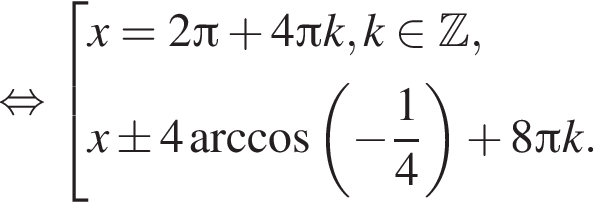
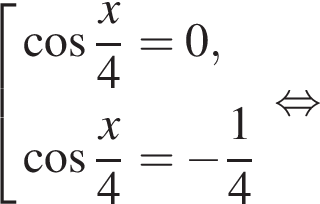
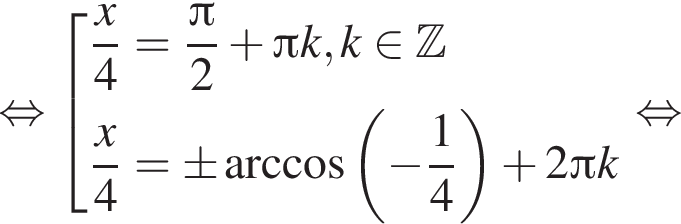

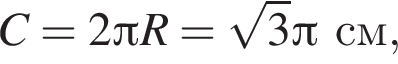 получим
получим 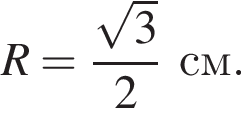
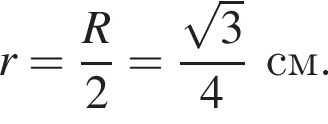
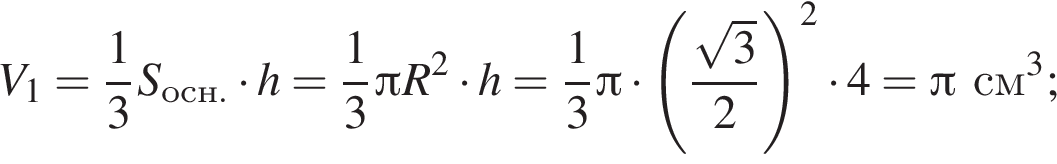
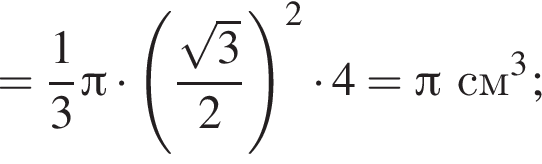
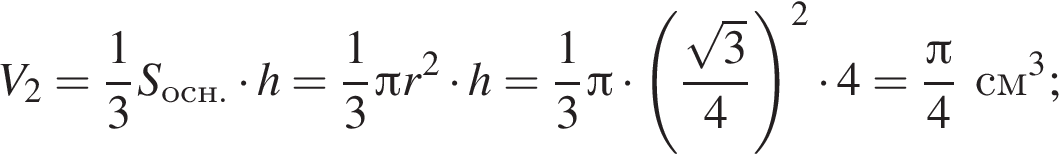
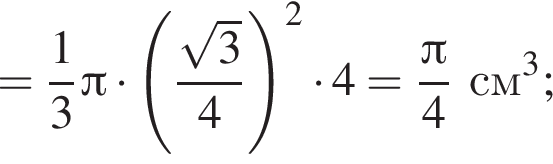
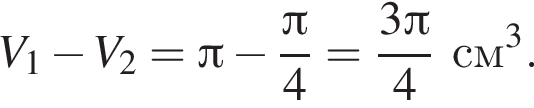
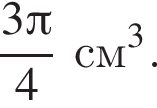
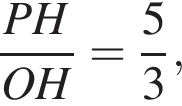 а значит,
а значит, 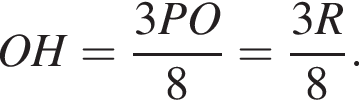
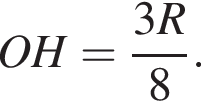 По теореме Пифагора
По теореме Пифагора 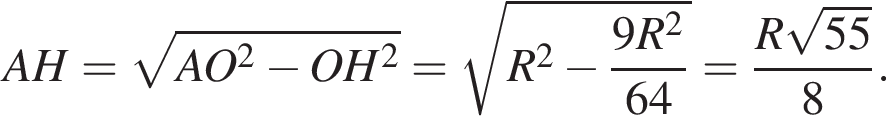
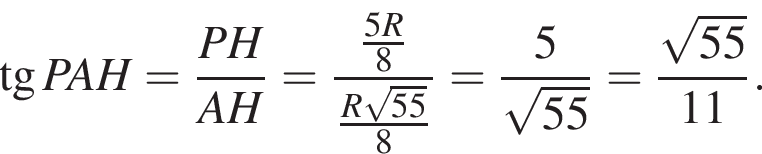
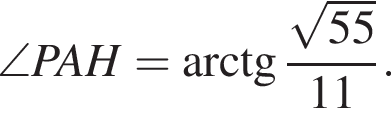
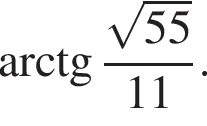
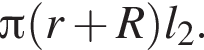 Пусть отношение меньшего из отрезков высоты ко всей высоте равно k, тогда равенство площадей можно представить как
Пусть отношение меньшего из отрезков высоты ко всей высоте равно k, тогда равенство площадей можно представить как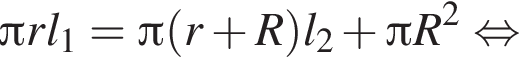
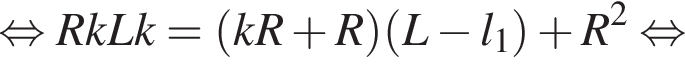
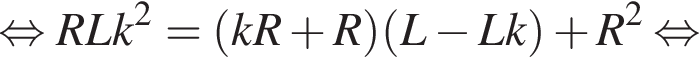
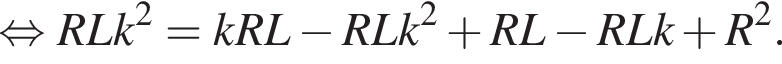
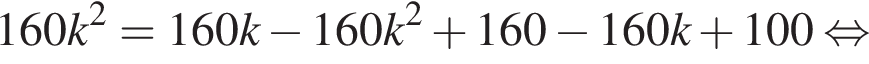
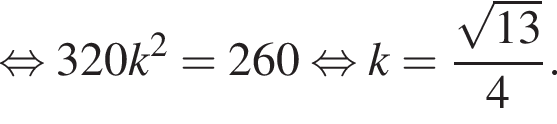
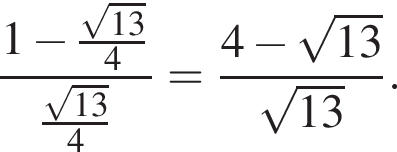
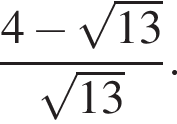
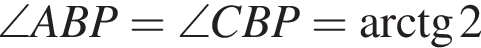 и
и  Также проведены высоты PF и PM к сторонам основания и высота пирамиды
Также проведены высоты PF и PM к сторонам основания и высота пирамиды 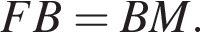 Так как HB — общая сторона, то треугольники BHF и BHM равны по катету и гипотенузе. Тогда
Так как HB — общая сторона, то треугольники BHF и BHM равны по катету и гипотенузе. Тогда  и BH — биссектриса
и BH — биссектриса 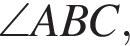 следовательно,
следовательно, 

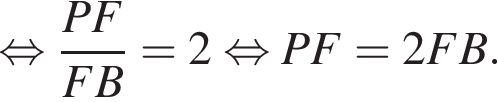
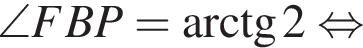
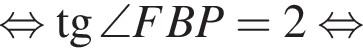
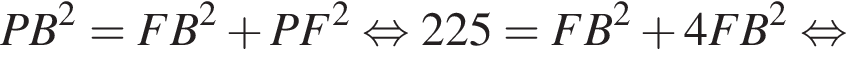

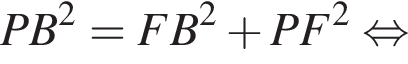
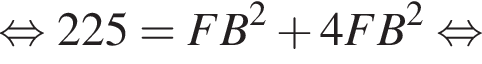
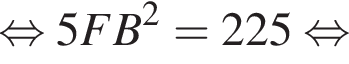
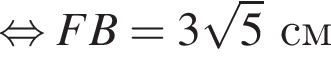
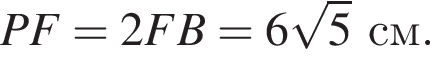
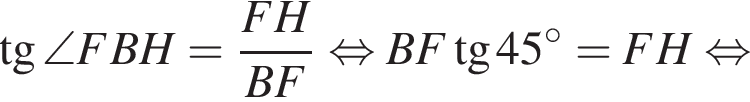
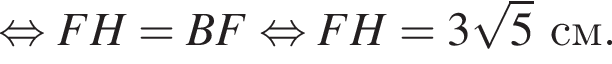
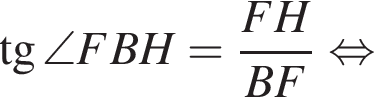

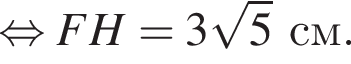
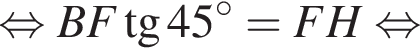
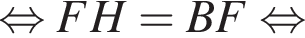
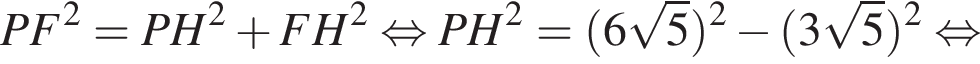
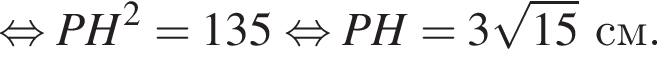
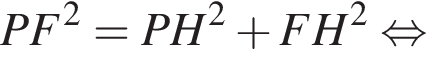
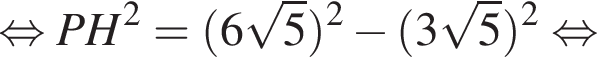
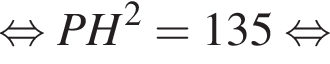
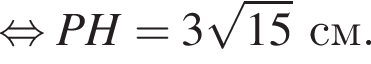
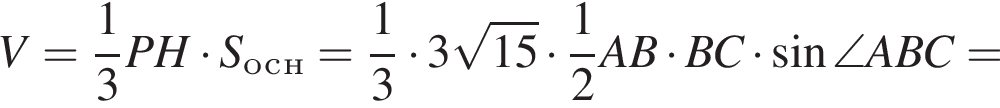
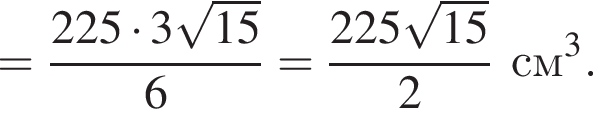

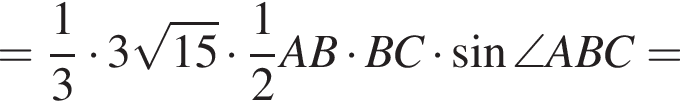
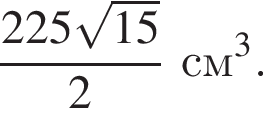
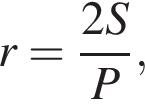 где P — периметр основания призмы. Тогда высота призмы равна
где P — периметр основания призмы. Тогда высота призмы равна 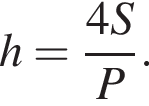 Площадь полной поверхности призмы равна:
Площадь полной поверхности призмы равна: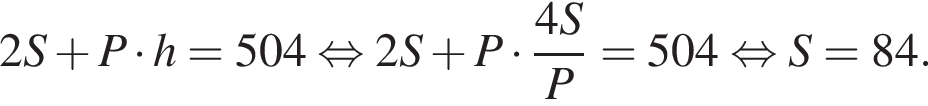
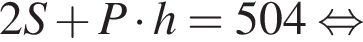
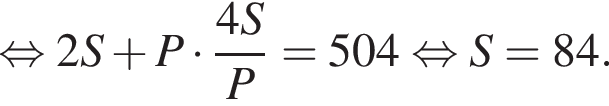
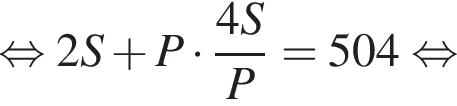

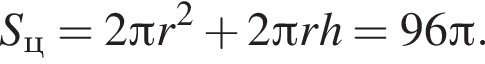
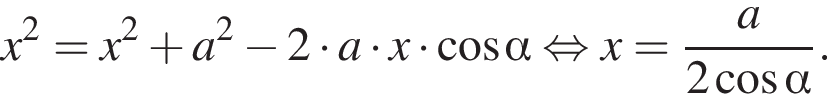
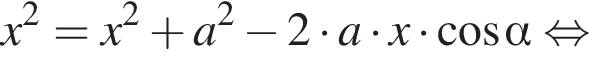
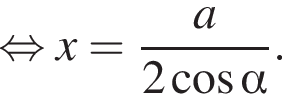
 и
и 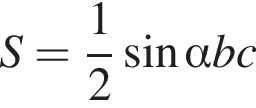 получаем
получаем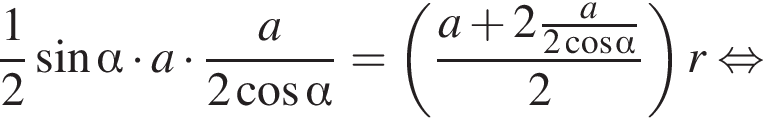
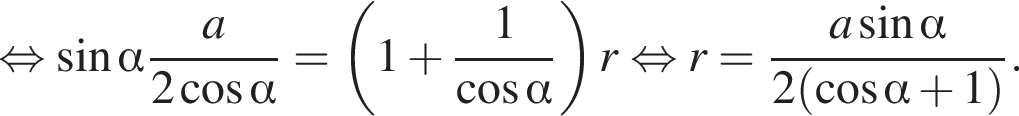
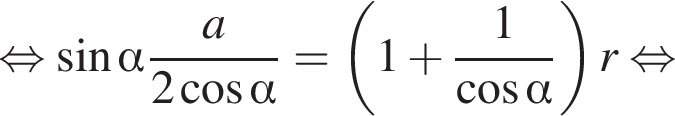
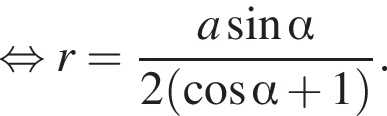
 то есть
то есть 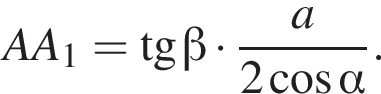 Используя формулу площади боковой поверхности цилиндра имеем
Используя формулу площади боковой поверхности цилиндра имеем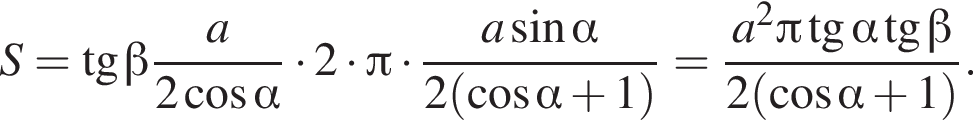
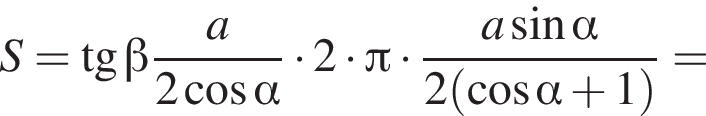
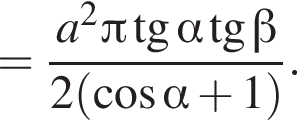
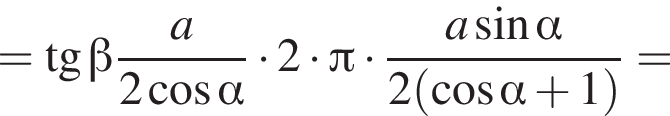
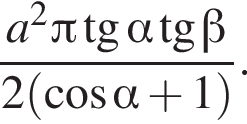
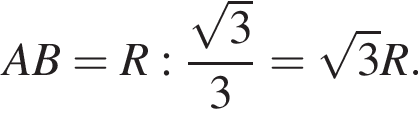
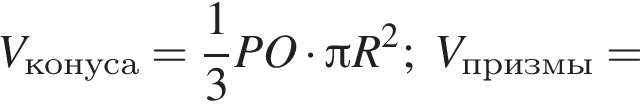
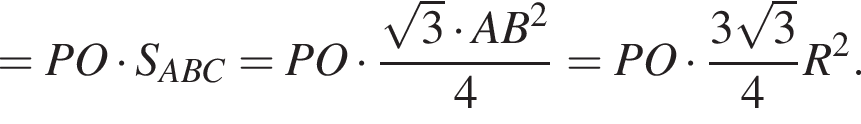
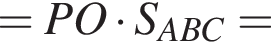
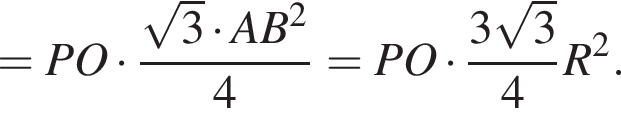

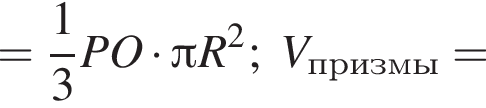
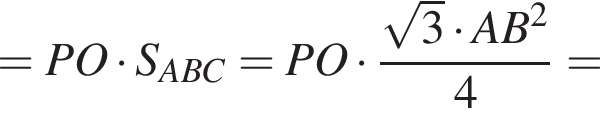
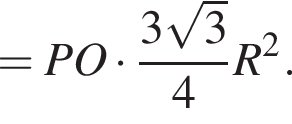
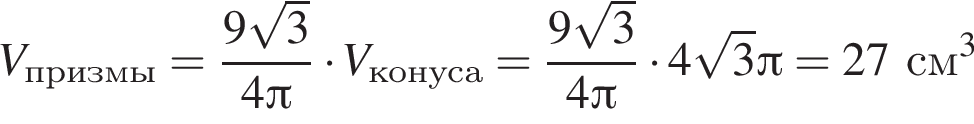
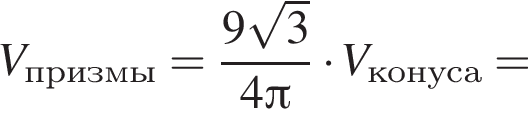
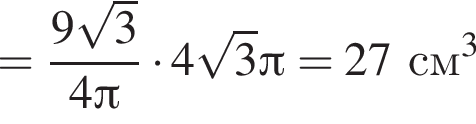
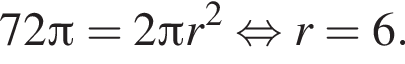
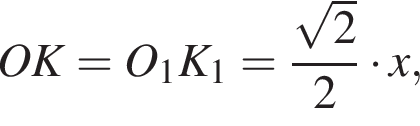
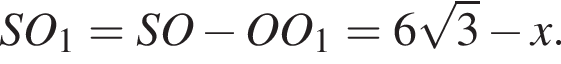
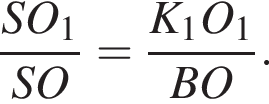
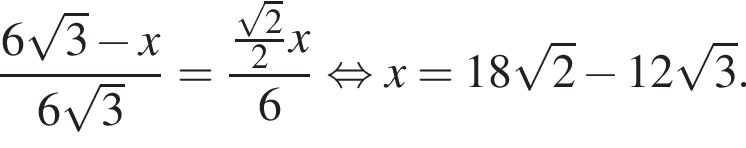
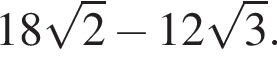
 Треугольник AKB — равнобедренный (AK = BK), тогда
Треугольник AKB — равнобедренный (AK = BK), тогда  Воспользуемся теоремой синусов:
Воспользуемся теоремой синусов: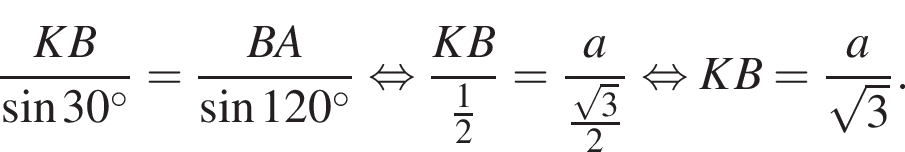
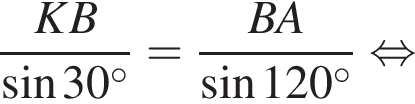
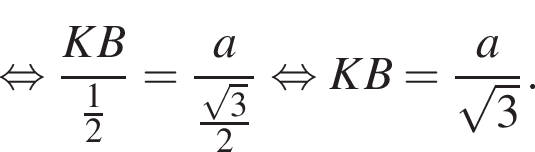
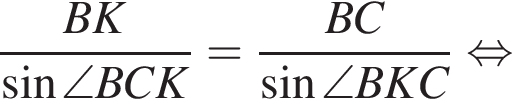
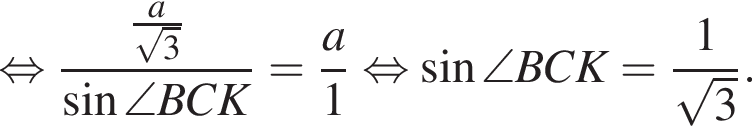
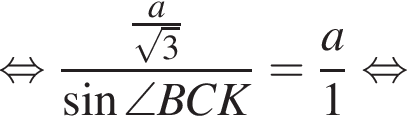
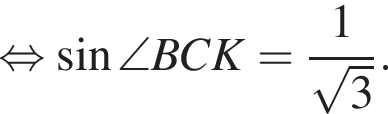
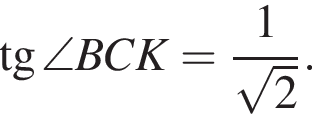
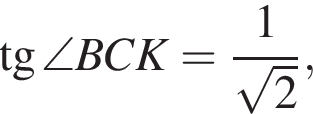 тогда
тогда 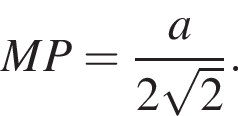 Так как треугольник ABC равносторонний, то H — центр треугольника, откуда
Так как треугольник ABC равносторонний, то H — центр треугольника, откуда 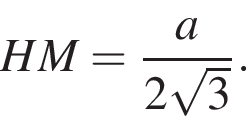
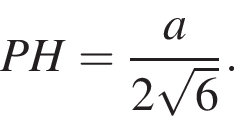 По условию высота пирамиды равна 3, тогда:
По условию высота пирамиды равна 3, тогда: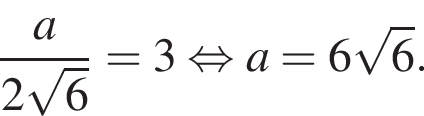
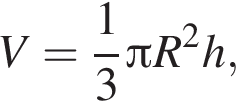 где
где 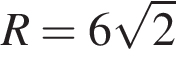 и h = 3:
и h = 3: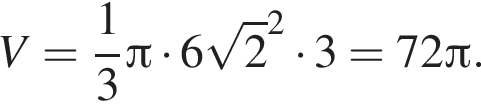
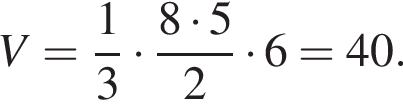 Так как треугольники ABC и A1B1C1 подобны, причем коэффициент подобия равен
Так как треугольники ABC и A1B1C1 подобны, причем коэффициент подобия равен 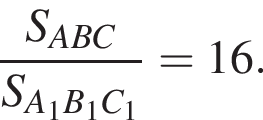 Тогда объем маленькой пирамиды V1 равен:
Тогда объем маленькой пирамиды V1 равен: 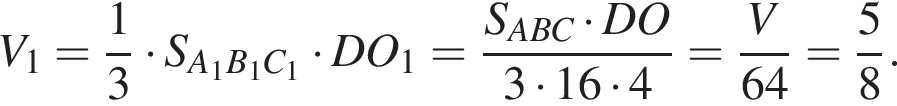
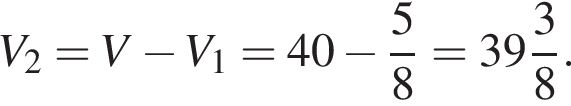

 ADC — основание пирамиды. По теореме Пифагора в треугольнике ADC гипотенуза AC равна
ADC — основание пирамиды. По теореме Пифагора в треугольнике ADC гипотенуза AC равна 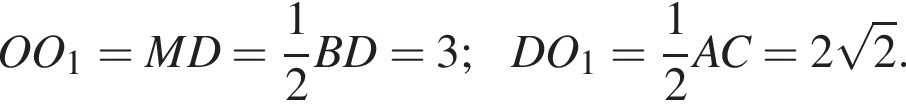
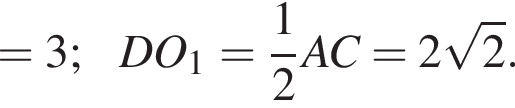
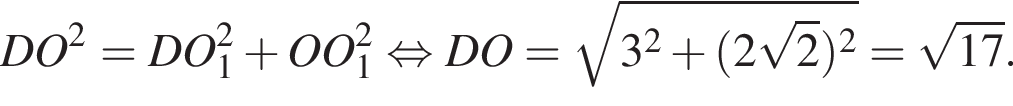
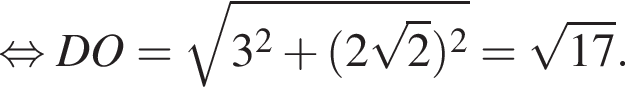

 Аналогично, для треугольников BHC и DHC имеем
Аналогично, для треугольников BHC и DHC имеем  Тогда
Тогда 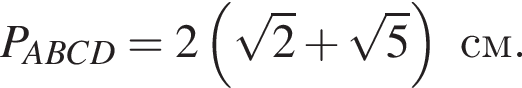
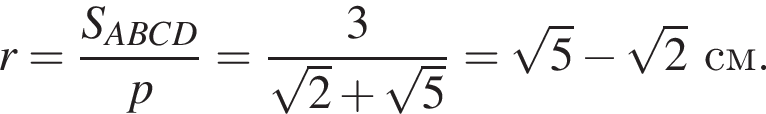
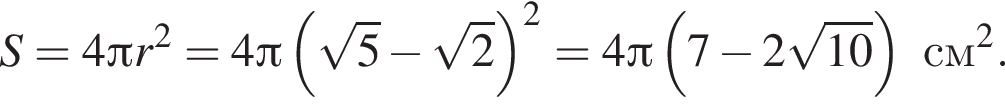
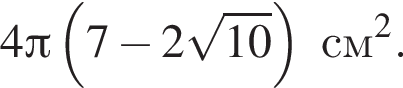
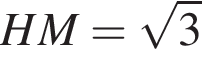 см, а
см, а  см.
см. см и
см и 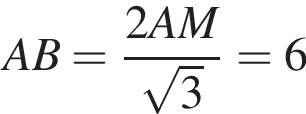 см.
см.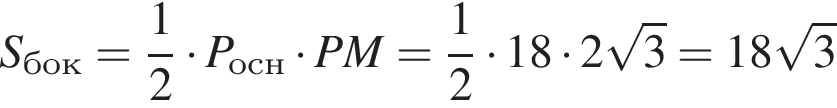
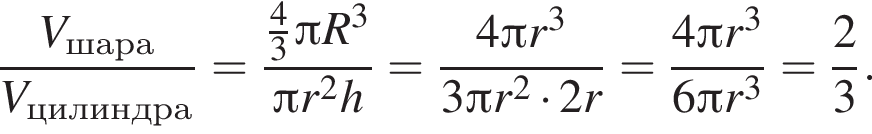
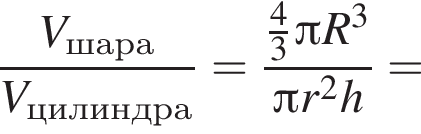
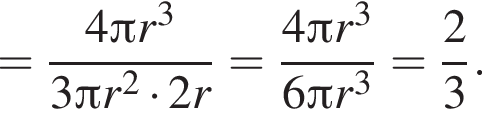
 В треугольниках FAN и LAM угол
В треугольниках FAN и LAM угол  и
и  — прямые, значит, эти треугольники подобны по двум углам, откуда:
— прямые, значит, эти треугольники подобны по двум углам, откуда: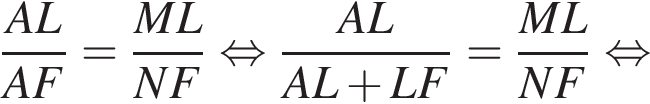
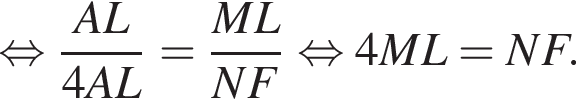
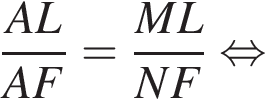
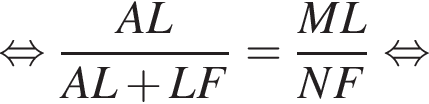
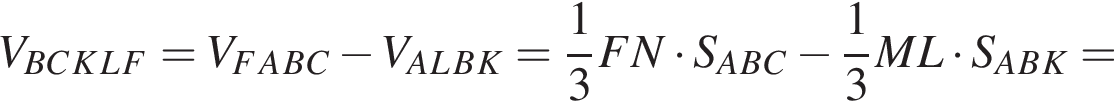

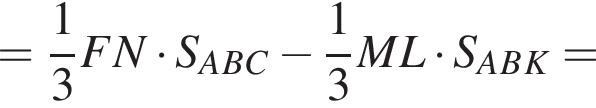
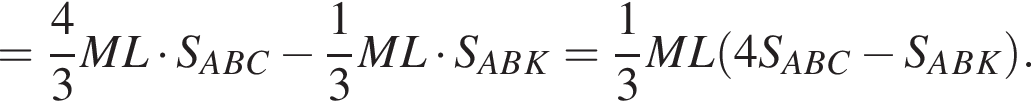
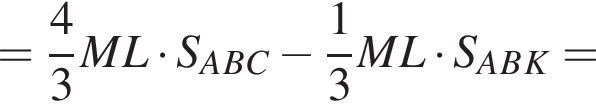
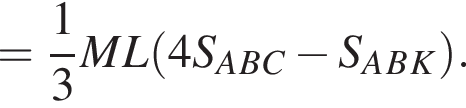
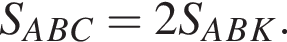 Тогда:
Тогда: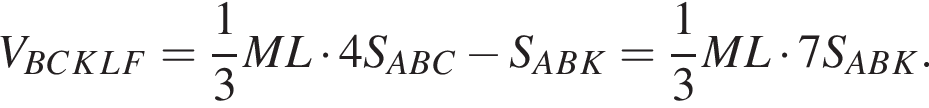
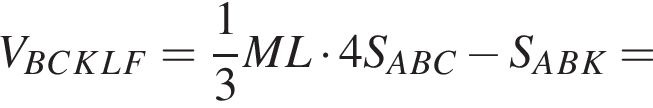
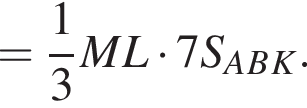

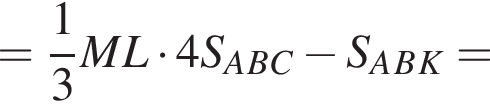
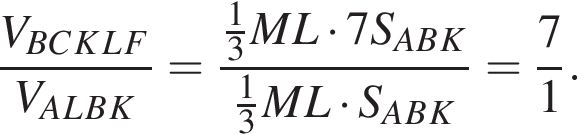
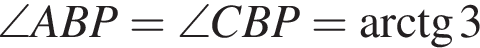 и
и  Также проведены высоты PF и PM к сторонам основания и высота пирамиды
Также проведены высоты PF и PM к сторонам основания и высота пирамиды 

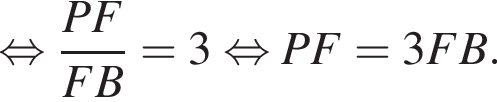
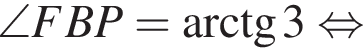
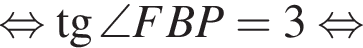
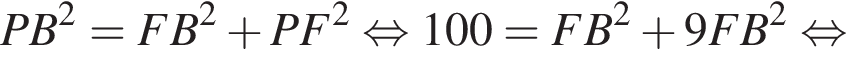

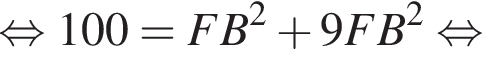
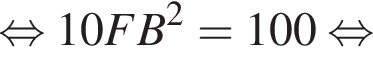

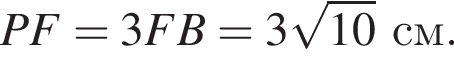
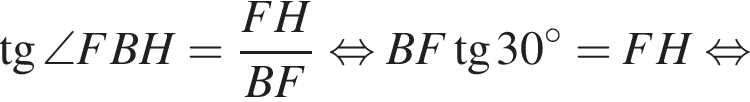
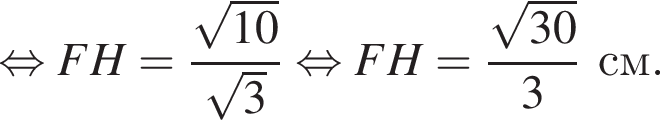

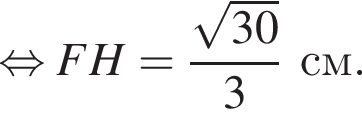

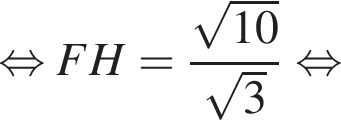
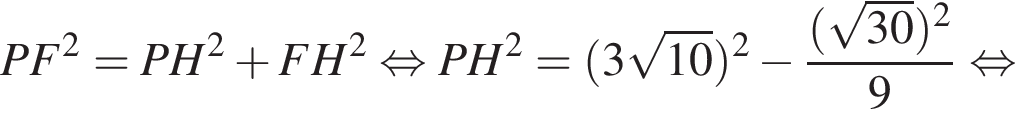

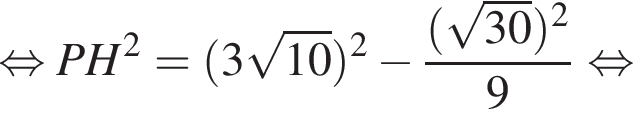
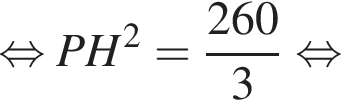
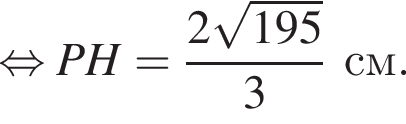
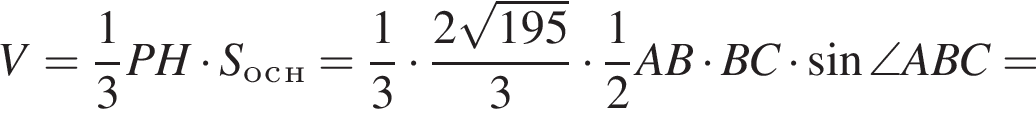
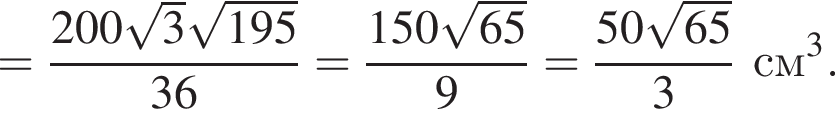
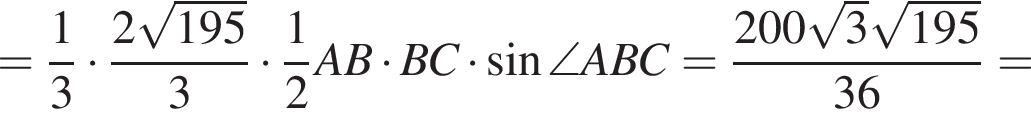
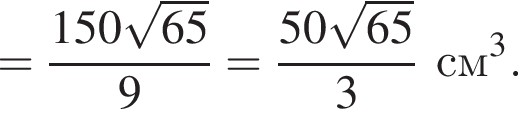
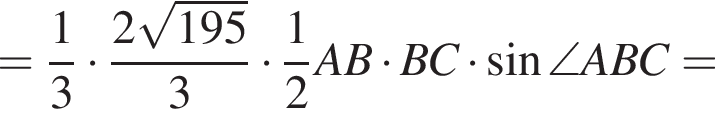
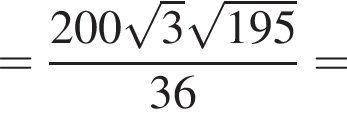
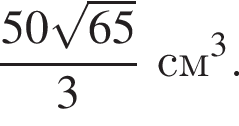
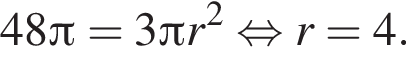
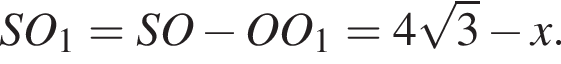
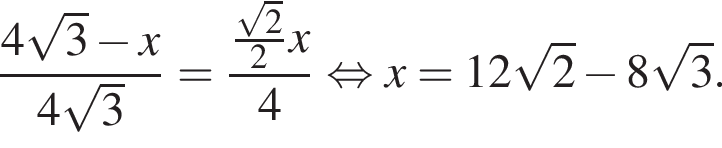
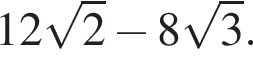
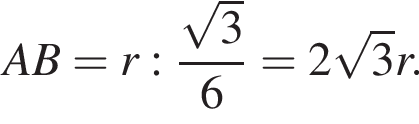
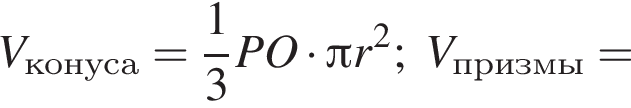
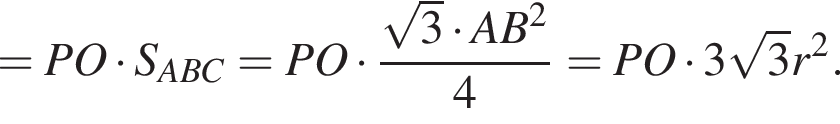
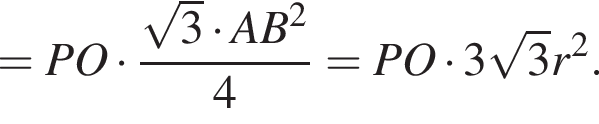
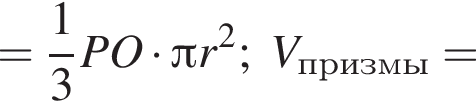
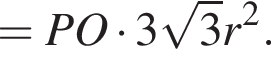
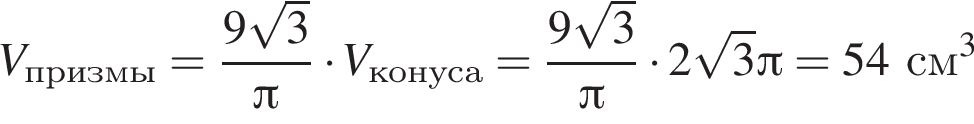
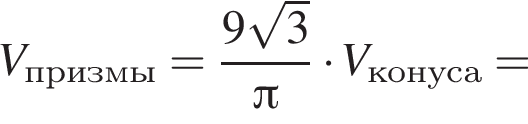
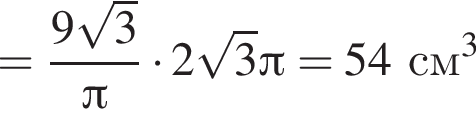
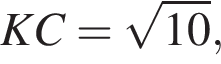 а
а  Отрезки XA и AB равны, так как AK — средняя линия треугольника XBC. В треугольнике XBM отрезок EA вляется средней линием, так как XA = AB и EA параллельно MB. Это значит, что
Отрезки XA и AB равны, так как AK — средняя линия треугольника XBC. В треугольнике XBM отрезок EA вляется средней линием, так как XA = AB и EA параллельно MB. Это значит, что 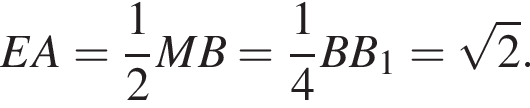 В треугольниках EAK и XBM по теореме Пифагора получаем, что
В треугольниках EAK и XBM по теореме Пифагора получаем, что 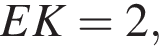 а
а 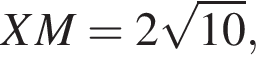 тогда
тогда 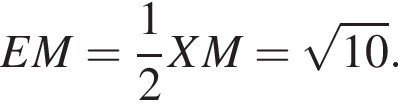 Периметр сечения равен:
Периметр сечения равен:

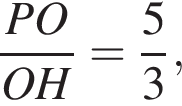 а значит,
а значит, 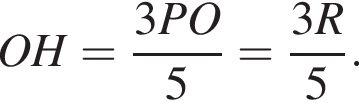
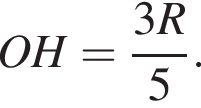 По теореме Пифагора
По теореме Пифагора 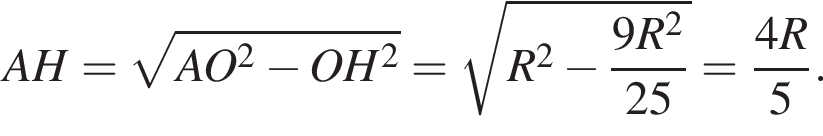
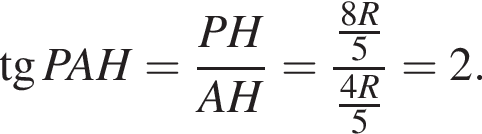


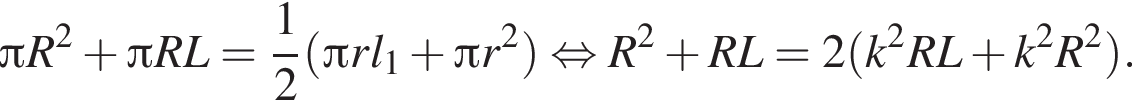
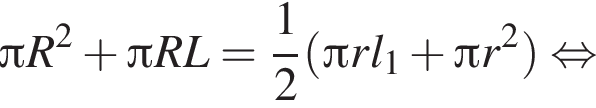
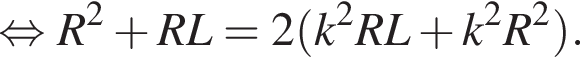
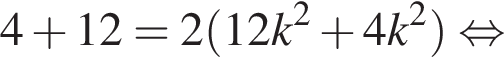
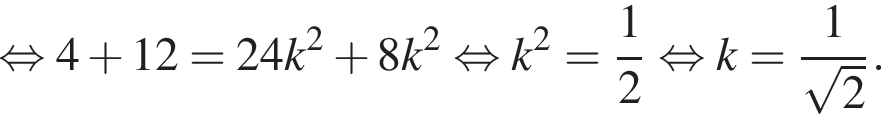
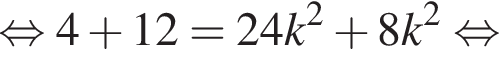
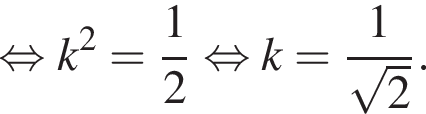
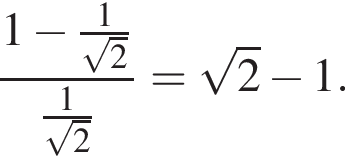
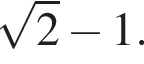
 Пусть его сторона равна
Пусть его сторона равна 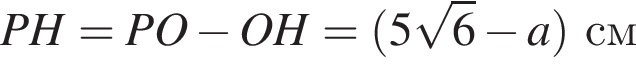
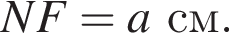 Рассмотрим треугольники PTM и PNF. В них
Рассмотрим треугольники PTM и PNF. В них  — общий, а
— общий, а  как соответственные углы при параллельных прямых NF и TM (PT — секущая). Тогда эти треугольники подобны до двум углам, следовательно:
как соответственные углы при параллельных прямых NF и TM (PT — секущая). Тогда эти треугольники подобны до двум углам, следовательно: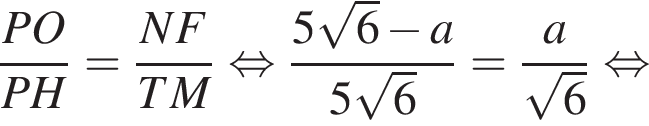
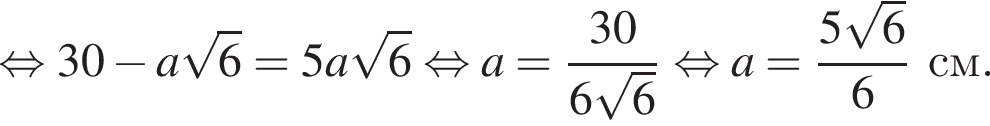
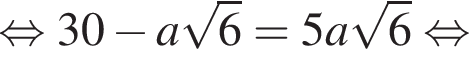
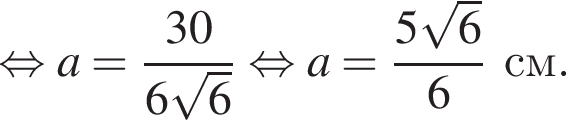
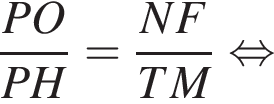
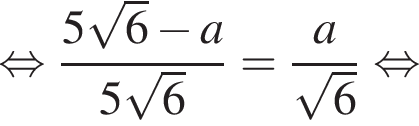
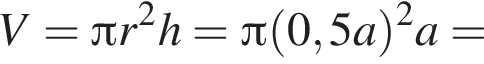
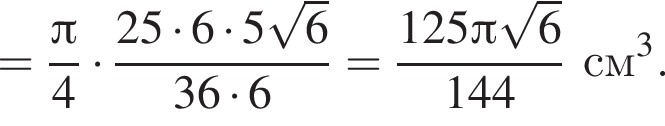
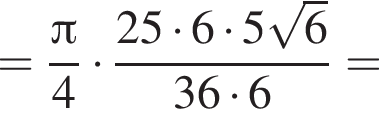
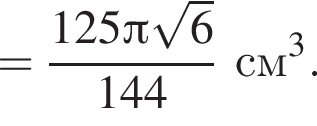
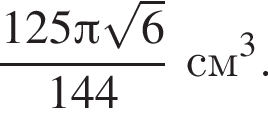
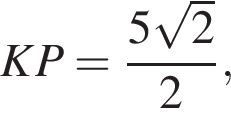 так как является средней линией треугольника BAC. Аналогично находим
так как является средней линией треугольника BAC. Аналогично находим 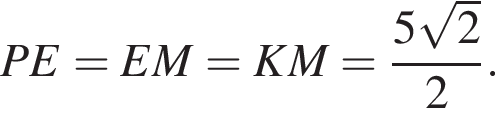 Четырёхугольник MKPE — квадрат, площадь которого равна
Четырёхугольник MKPE — квадрат, площадь которого равна 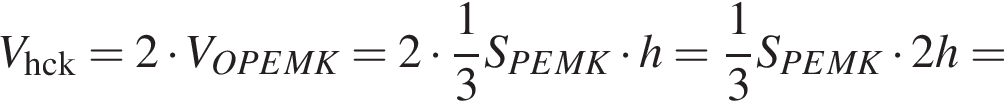
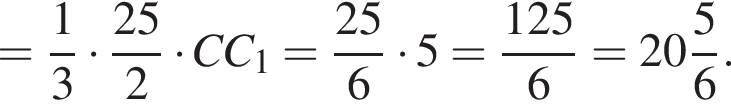
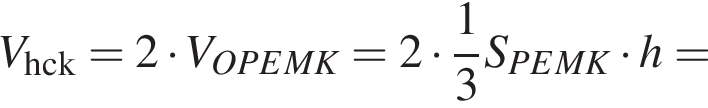
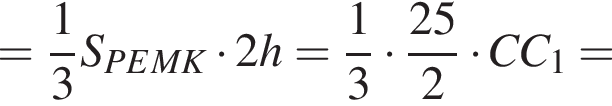
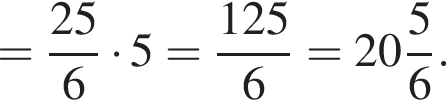

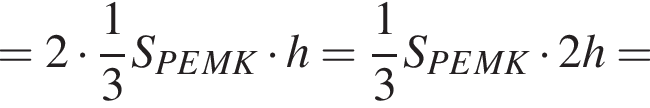
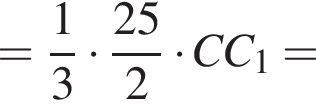

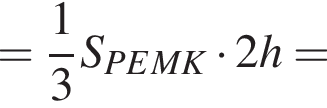
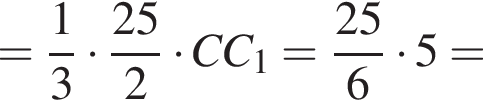
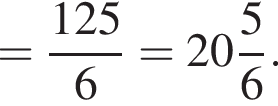
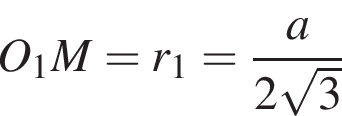 как радиус вписанной в основание окружности. Тогда
как радиус вписанной в основание окружности. Тогда 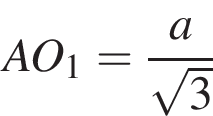 как радиус описанной около основания окружности. Имеем:
как радиус описанной около основания окружности. Имеем: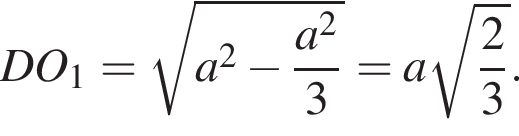
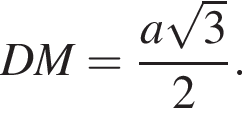
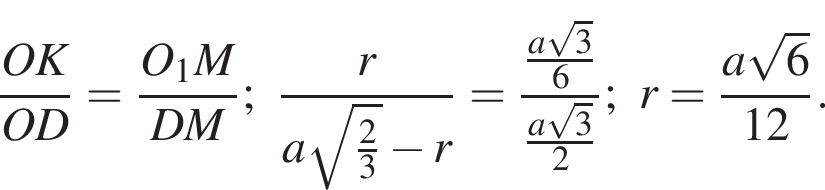
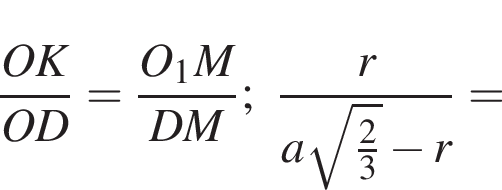
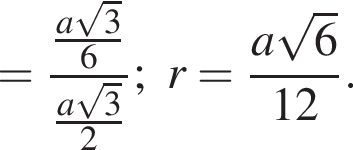


 Треугольник KOP прямоугольный,
Треугольник KOP прямоугольный, 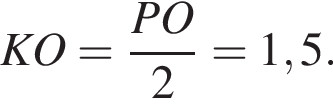 В прямоугольном треугольнике KHO KO = 1,5,
В прямоугольном треугольнике KHO KO = 1,5, 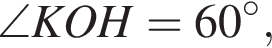 тогда
тогда 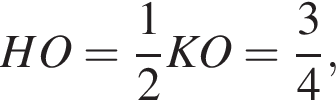
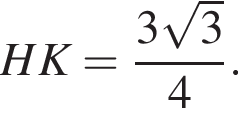 Найдем объем вписанного конуса:
Найдем объем вписанного конуса: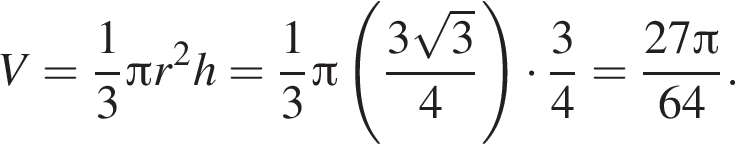
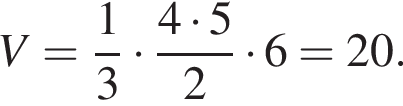 Так как треугольники ABC и A1B1C1 подобны, причем коэффициент подобия равен
Так как треугольники ABC и A1B1C1 подобны, причем коэффициент подобия равен 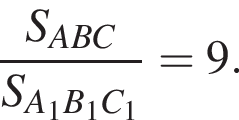 Тогда объем маленькой пирамиды V1 равен:
Тогда объем маленькой пирамиды V1 равен: 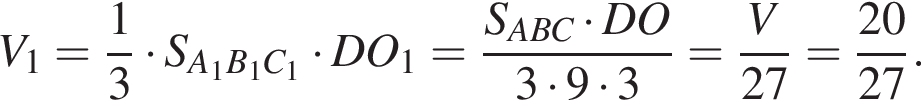
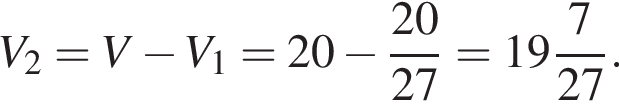
 и
и  как радиус проведенный к касательной.
как радиус проведенный к касательной. Катет KM прямоугольного треугольника OKM равен половине гипотенузы, значит,
Катет KM прямоугольного треугольника OKM равен половине гипотенузы, значит, 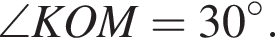
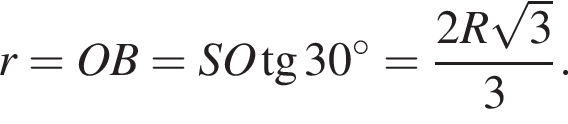 Так как SB образующая конуса в два раза больше радиуса его основания OB, то
Так как SB образующая конуса в два раза больше радиуса его основания OB, то 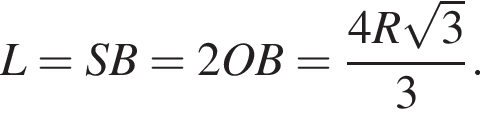

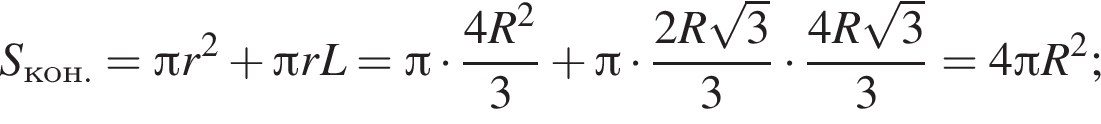
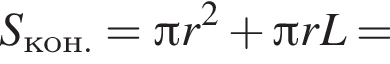
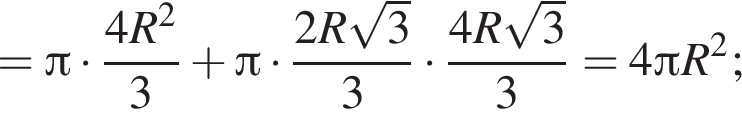
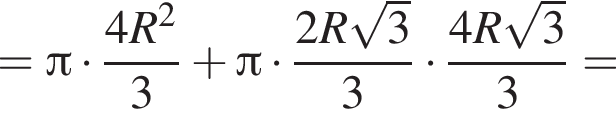
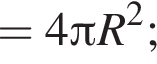
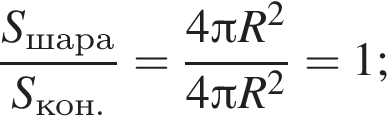
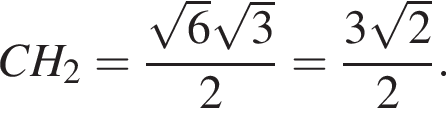
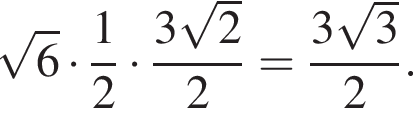 Найдём объём пирамиды
Найдём объём пирамиды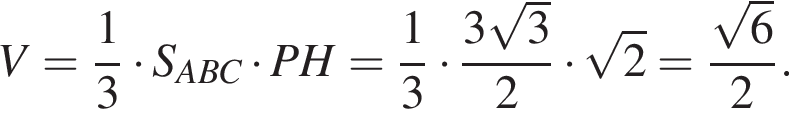
 аналогично
аналогично 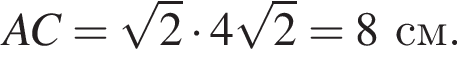 Из условия
Из условия  следовательно,
следовательно, 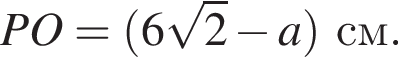 Подставим данные в отношения, полученные из подобия, и найдем a:
Подставим данные в отношения, полученные из подобия, и найдем a: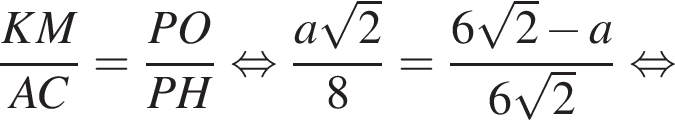
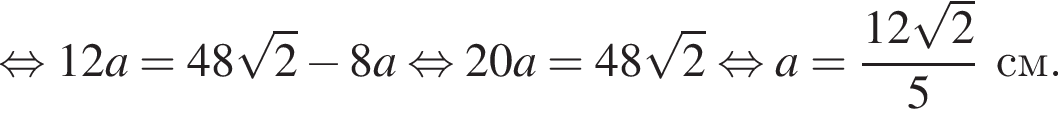
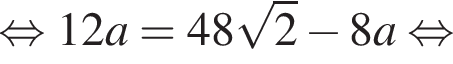
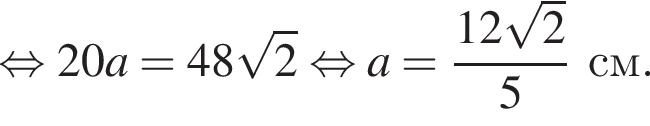
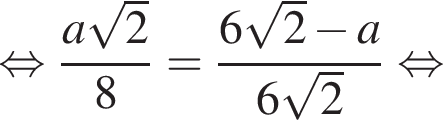
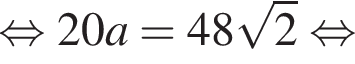
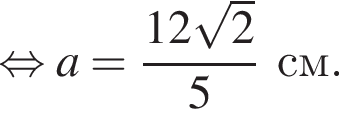
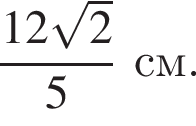
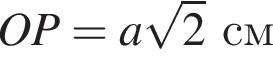 и
и  так как основание пирамиды — вписанный в окружность правильный треугольник. В прямоугольном треугольнике
так как основание пирамиды — вписанный в окружность правильный треугольник. В прямоугольном треугольнике 

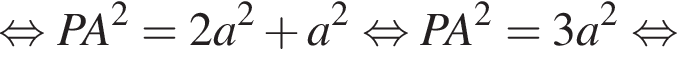
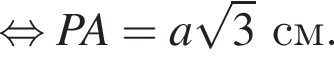
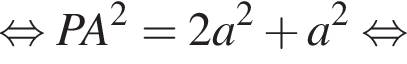

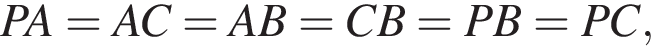
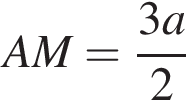 и
и  равен углу между боковыми гранями пирамиды. По теореме косинусов в треугольнике AMB:
равен углу между боковыми гранями пирамиды. По теореме косинусов в треугольнике AMB: 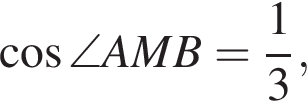 откуда
откуда 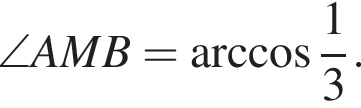
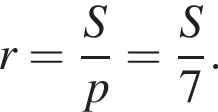
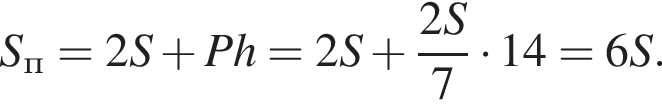 По условию Sпр = 56, значит,
По условию Sпр = 56, значит, 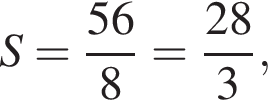 тогда
тогда 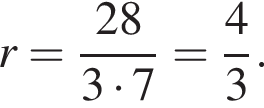 Найдём площадь боковой поверхности цилиндра:
Найдём площадь боковой поверхности цилиндра: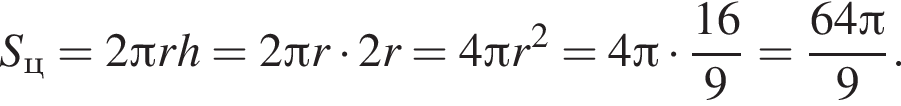

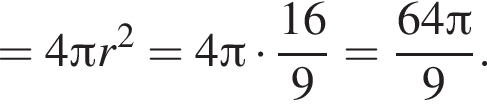

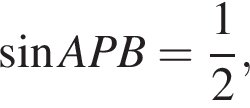 то есть угол APB равен 150°, исходя из того что по условию он тупой. Площадь Sосн основания конуса равна
то есть угол APB равен 150°, исходя из того что по условию он тупой. Площадь Sосн основания конуса равна  а площадь Sбок боковой поверхности —
а площадь Sбок боковой поверхности — 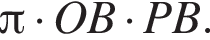 Две эти величины имеют следующее отношение:
Две эти величины имеют следующее отношение: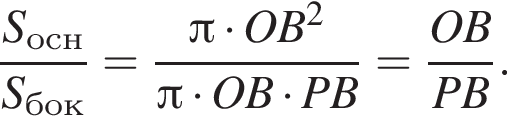
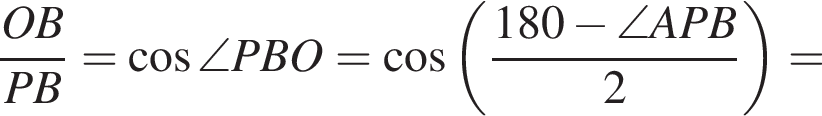
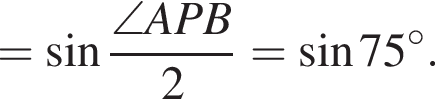
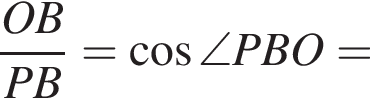
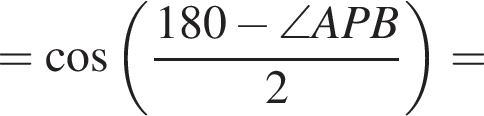
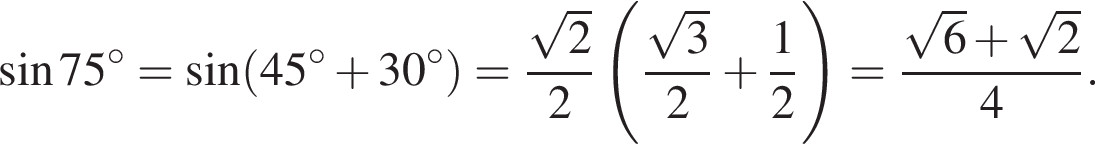
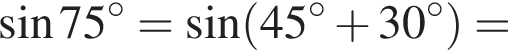
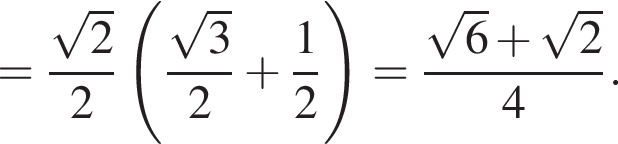
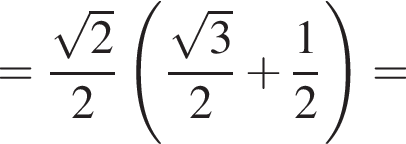
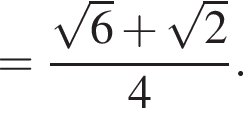
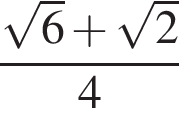 раза.
раза.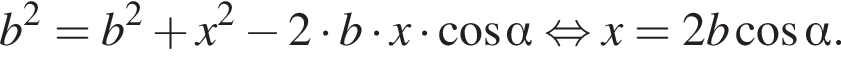
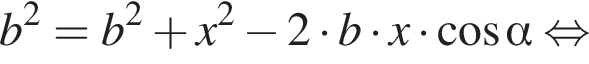

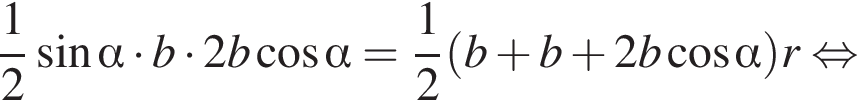
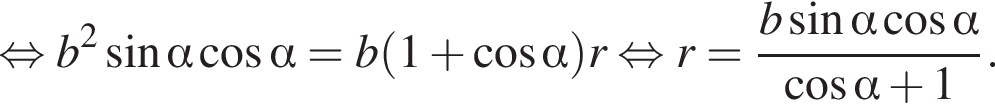

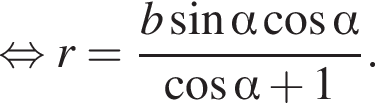
 то есть
то есть 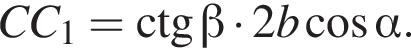 Используя формулу площади боковой поверхности цилиндра имеем
Используя формулу площади боковой поверхности цилиндра имеем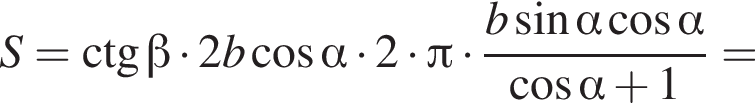
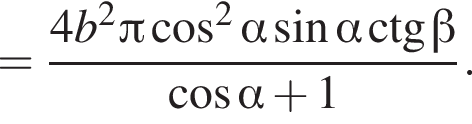
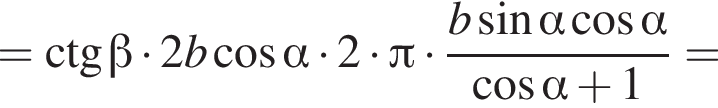
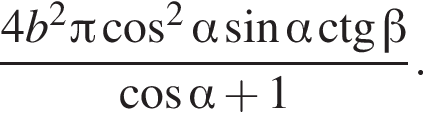
 Заметим, что OO1 — ось цилиндра, а M1 — точка касания верхнего основания цилиндра и апофемы. Получаем, что треугольник DOM равнобедренный. По условию OO1 = 2M1O1. Пусть AB = a, тогда:
Заметим, что OO1 — ось цилиндра, а M1 — точка касания верхнего основания цилиндра и апофемы. Получаем, что треугольник DOM равнобедренный. По условию OO1 = 2M1O1. Пусть AB = a, тогда: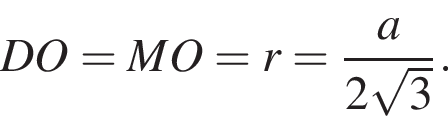
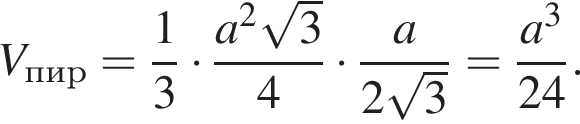
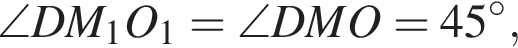 получаем, что DO1 = x, а DO = 3x. Тогда имеем:
получаем, что DO1 = x, а DO = 3x. Тогда имеем: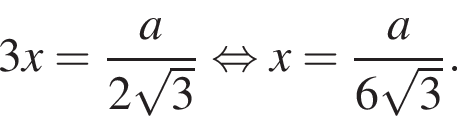
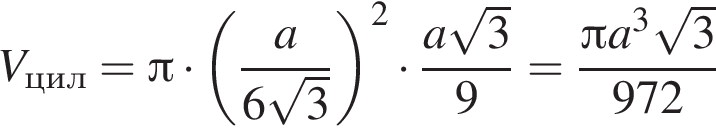
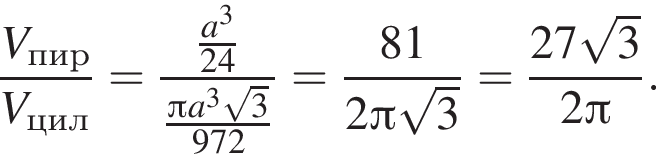
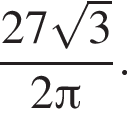
 а площадь поверхности шара получаем по формуле
а площадь поверхности шара получаем по формуле 
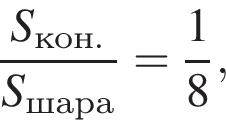 отсюда
отсюда 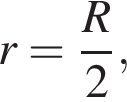 тогда в прямоугольном треугольнике OO1B имеем
тогда в прямоугольном треугольнике OO1B имеем 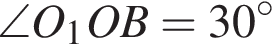 по свойству прямоугольных треугольников. Тогда
по свойству прямоугольных треугольников. Тогда 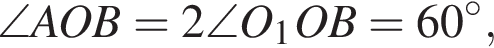 а значит, треугольник равносторонний. Найдем высоту OO1 по формуле высоты для правильных треугольников
а значит, треугольник равносторонний. Найдем высоту OO1 по формуле высоты для правильных треугольников 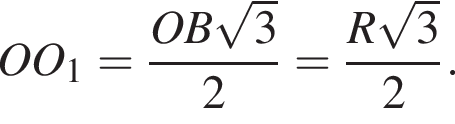
 В треугольниках FBN и LBM угол
В треугольниках FBN и LBM угол  — общий, а углы
— общий, а углы  и
и  — прямые, значит, эти треугольники подобны по двум углам, откуда:
— прямые, значит, эти треугольники подобны по двум углам, откуда: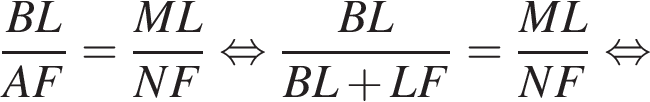
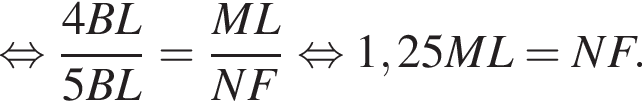
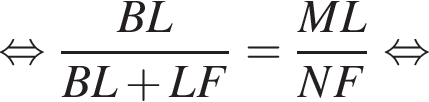
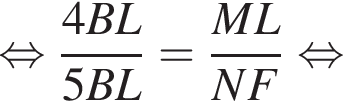

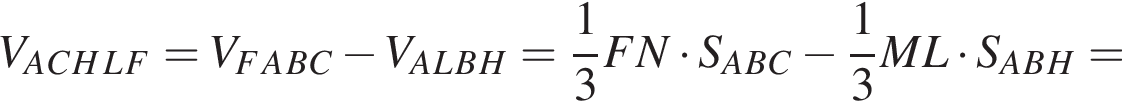

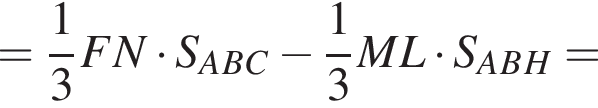
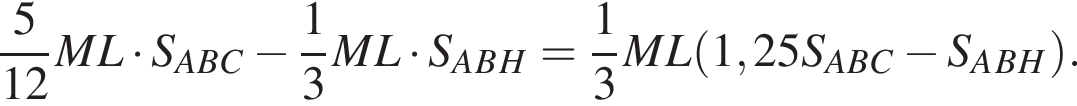

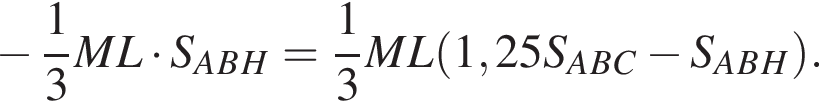
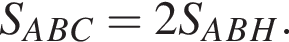 Тогда:
Тогда: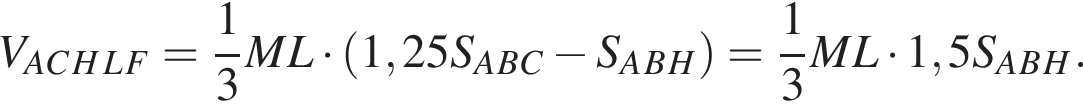
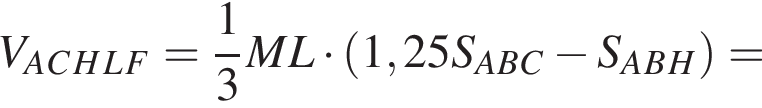
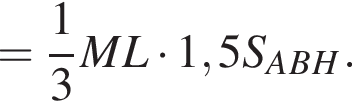

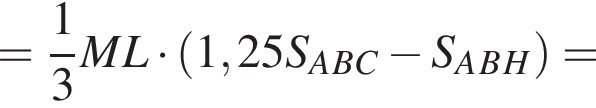
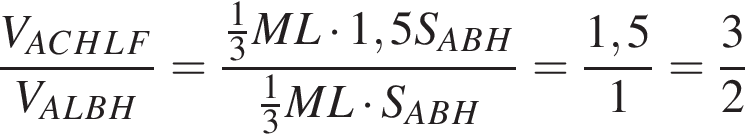
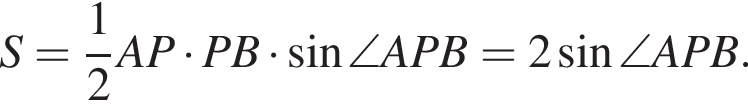
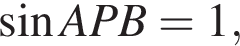 то есть угол APB равен 90°. Площадь Sосн основания конуса равна
то есть угол APB равен 90°. Площадь Sосн основания конуса равна  Две эти величины имеют следующее отношение:
Две эти величины имеют следующее отношение: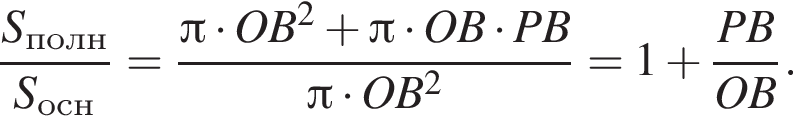
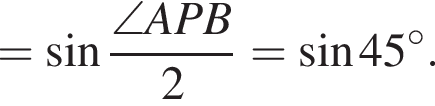
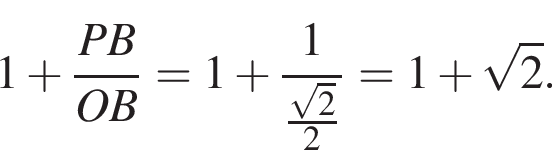
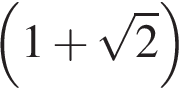 раз.
раз.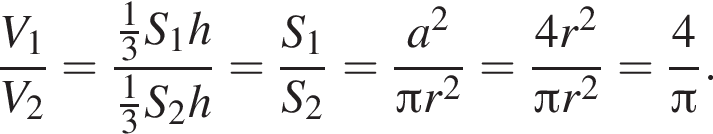
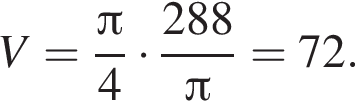
 тогда
тогда 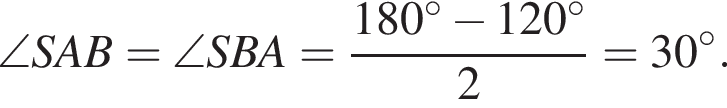
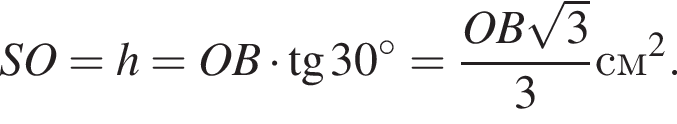
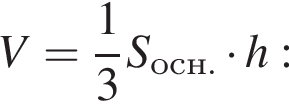
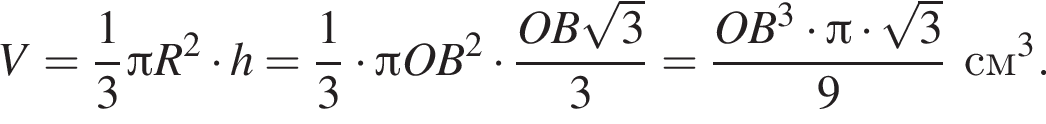
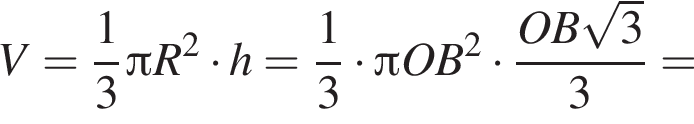
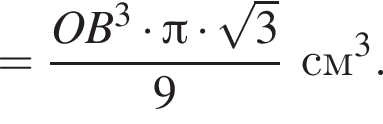
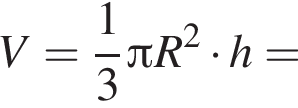
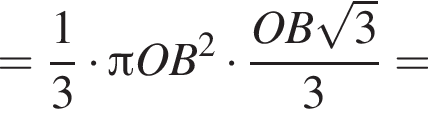
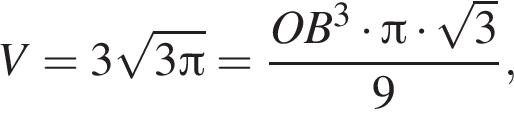 тогда OB = 3 см, AB = 2OB = 6 см.
тогда OB = 3 см, AB = 2OB = 6 см.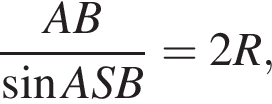 тогда
тогда 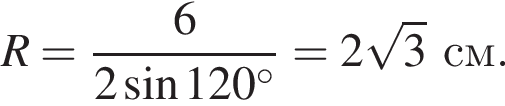
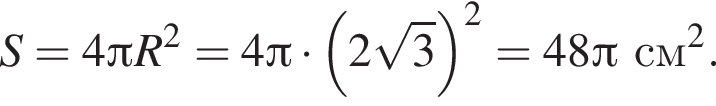

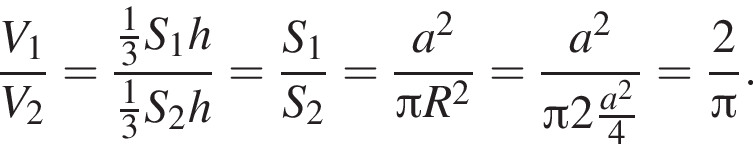
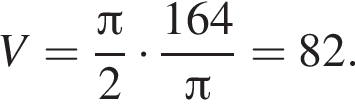
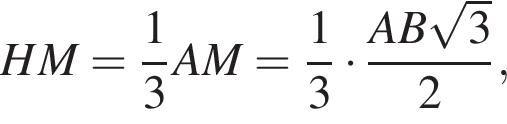
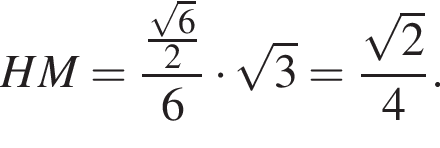
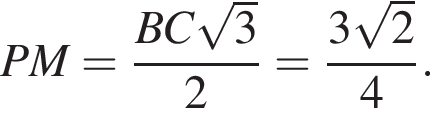
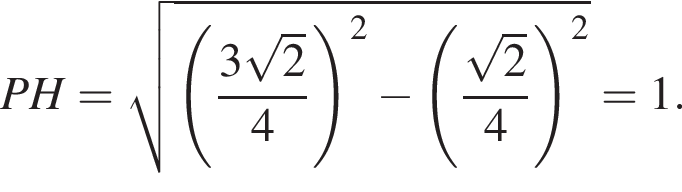
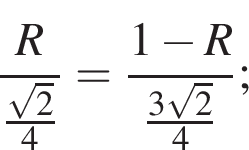
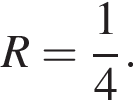
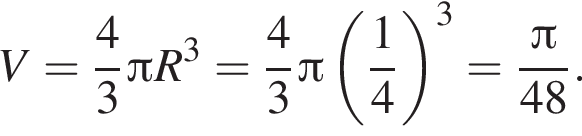
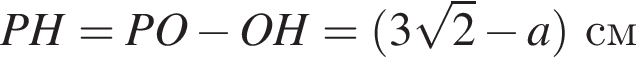
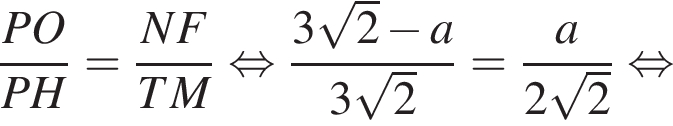
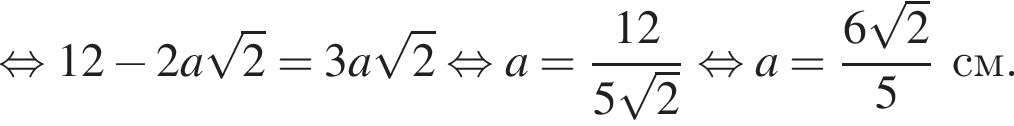
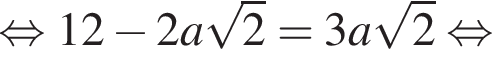
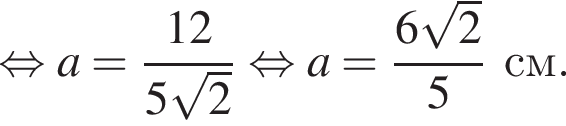
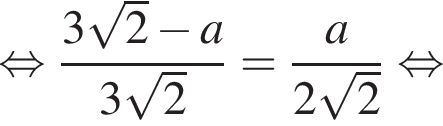
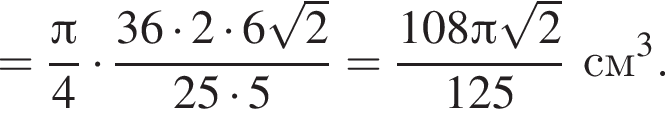
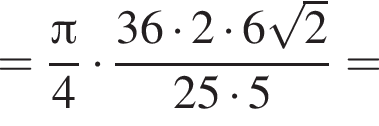
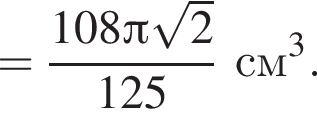
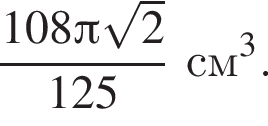
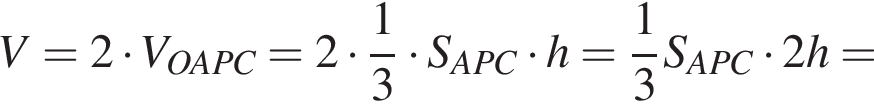
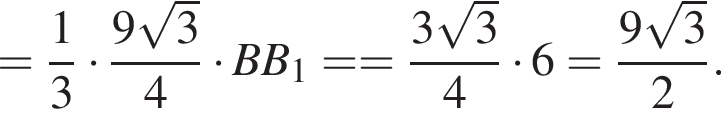
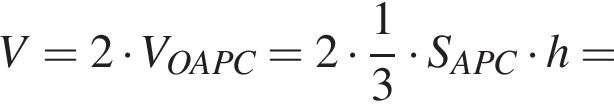
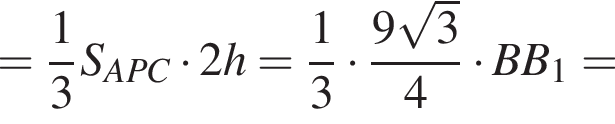
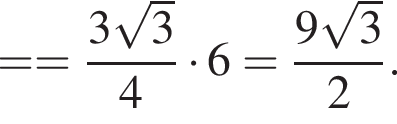
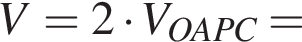
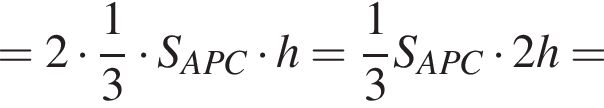
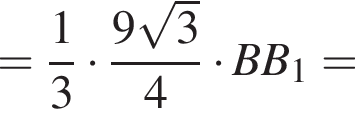
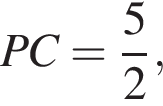 а
а  Отрезки XA и AB равны, так как AP — средняя линия треугольника XBC. В треугольнике XBM отрезок KA вляется средней линием, так как XA = AB и KA параллельно MB. Это значит, что
Отрезки XA и AB равны, так как AP — средняя линия треугольника XBC. В треугольнике XBM отрезок KA вляется средней линием, так как XA = AB и KA параллельно MB. Это значит, что 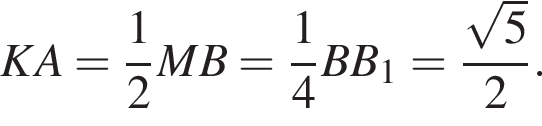 В треугольниках KAP и XBM по теореме Пифагора получаем, что
В треугольниках KAP и XBM по теореме Пифагора получаем, что 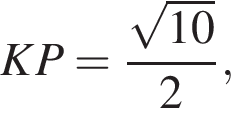 а XM = 5, тогда
а XM = 5, тогда 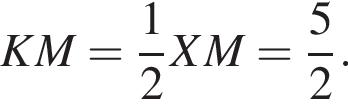 Периметр сечения равен:
Периметр сечения равен: 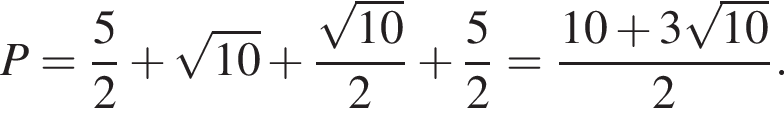
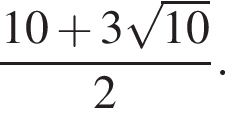
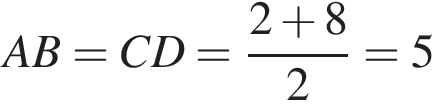 см.
см.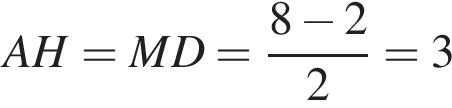 см.
см. см2.
см2.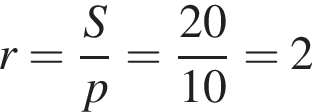 см.
см. 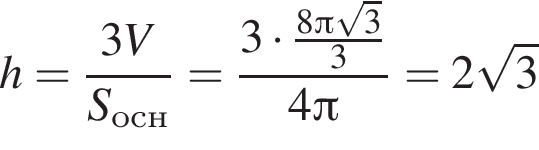 см.
см.